Ayant l'âme d'un étudiant en art, l'un de vos passe-temps favoris est de vous ballader dans la galerie d'art locale en y contemplant les diverses créations qui s'y trouvent. Un jour, vous imaginez ce que cela pourrait donner de paver l'entrée de votre résidence pour qu'elle ressemble à l'un de ces tableaux. Vous sortez donc votre appareil photo numérique et prenez un cliché de l'un de vos tableaux préférés. Malheureusement, avec votre maladresse habituelle, vous avez accidentellement laissé votre filtre bleu sur l'objectif et la photo que vous avez prise est composée uniquement de nuances de bleu.

Ceci ne vous décourage cependant pas, car l'idée d'une entrée carrelée en bleu vous parait tout à fait intéressante. Après avoir fait le tour du marchand de carreaux du coin, vous trouvez un certain nombre de carreaux bleus que vous pouvez utiliser. Tous les carreaux sont carrés et ont comme taille 1m x 1m, 2m x 2m, 3m x 3m ou 4m x 4m. Chaque carreau est coloré d'une seule nuance de bleu, que vous pouvez mesurer par un entier allant de 0 (bleu très sombre) à 255 (bleu très clair). Chaque pixel de votre photo peut également être mesuré de 0 à 255 sur cette même échelle.

Votre objectif est de disposer un certain nombre de ces carreaux dans l'entrée de votre résidence, où une portion de 1m x 1m de carreau correspond à un pixel de votre photo. L'erreur pour chaque pixel est la valeur absolue de la différence entre la nuance de bleu de ce pixel et celle de la partie de carreau correspondante. L'erreur totale pour l'ensemble de la photo est la somme des erreurs individuelles de tous les pixels. Vous devez faire ressembler votre entrée autant que possible à la photo, i.e. vous devez rendre l'erreur totale aussi petite que possible.

Des carreaux ne peuvent pas se superposer et ne peuvent pas dépasser les bords de l'image. Vous ne pouvez pas laisser de trous (i.e., de pixels de votre photo pour lesquels ne correspondent pas de parties de carreau). Bien que le magasin ne propose que quelques types de carreaux différents, vous pouvez acheter autant de carreaux de chaque type que vous le souhaitez.

• 1 <= N <= 20, où N est le nombre de types de carreaux vendus.
• 1 <= S <= 4, où S est la longueur du côté (en mètres) d'un carreau.
• 0 <= K <= 255 où K est la nuance de bleu d'un carreau.
• 1 <= H, W <= 200, où H et W sont respectivement la hauteur et la longueur de l'image que vous devez dupliquer.

Les données d'entrée seront lues sur l'entrée standard. La première ligne est un entier N, indiquant le nombre de types de carreaux vendus par le magasin. Ces types sont numérotés 1,2,...,N.

Chacune des N lignes suivantes représente un type de carreau vendu. Chacune de ces lignes prendra la forme S K, où S représente la longueur du côté (en mètres) du carreau et K est un entier représentant sa nuance de bleu. On vous garantit qu'il y aura toujours au moins un carreau de dimension 1m x 1m fourni dans l'entrée.

La ligne suivante contient deux entiers, H et W séparés par un espace, où H est la hauteur de l'image que vous voulez dupliquer et W est sa largeur. Ceci est suivi de H lignes de W entiers (séparés par des espaces), représentant la nuance de bleu de chaque pixel de l'image. Chacun de ces entiers sera entre 0 et 255 inclus.

Votre programme doit écrire la meilleure solution qu'il pourra trouver, sur la sortie standard. Chaque ligne de la sortie représente la position d'un carreau et a la forme R C T, où R et C sont la ligne et la colonne du coin en haut à gauche du carreau (1 <= R <= H) et (1 <= C <= W) et T est le numéro du type de carreau que vous utilisez (1 <= T <= N). Vous pouvez afficher ces carreaux dans l'ordre que vous souhaitez.

Après avoir décrit les carreaux, votre programme doit écrire une ligne supplémentaire, contenant un entier : l'erreur totale de votre solution.

3
1 10
2 15
1 20
3 4
16 15 10 25
14 15 14 30
10 10 30 11

1 1 2
3 1 1
3 2 1
1 3 1
1 4 3
2 3 2
42

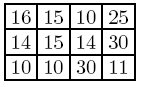
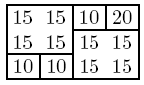
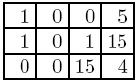
Les trois diagrammes suivants correspondent aux données d'exemple ci-dessus. La grille de gauche est la photo que vous devez reproduire avec une erreur totale aussi faible que possible. La grille du centre est un pavage possible utilisant les carreaux fournis. La grille de droite montre l'erreur résultante pour chaque pixel de la photographie.



La somme des erreurs pour chaque pixel est 1+0+0+5+1+0+1+15+0+0+15+4=42 et l'erreur totale pour ce pavage est de 42.

Calcul du score

Il n'y a pas de "meilleure solution" particulière que vous devez atteindre. Votre score sera déterminé relativement aux solutions des autres candidats (ainsi qu'à celle des juges). Pour chaque test, le candidat qui obtient l'erreur totale la plus faible est identifié. Votre score pour ce test est alors :

• 100% si votre programme trouve une solution ayant la même erreur totale;
• 10% si votre programme utilise pour chaque pixel le carreau de 1m x 1m dont la nuance de bleu est la plus proche (en ignorant les carreaux de tailles 2m x 2m et supérieures);
• 0% si votre programme génère une solution invalide;
• sinon, déterminé par une échelle linéaire relativement à votre erreur totale, où les notes 100% et 10% correspondent aux solutions décrites ci-dessus. Si votre solution décrit un pavage valide, aussi grande votre erreur totale soit-elle, on vous garantit au moins 5%.

Par exemple, pour l'exemple ci-dessus, l'erreur totale obtenue en faisant correspondre à chaque pixel, le carreau de 1m x 1m de nuance de bleu la plus proche, est de 48. Si la meilleure solution trouvée par un candidat (ou les juges) a une erreur totale de 32, alors l'échelle de score pour une solution valide sera la suivante :