Comme vous êtes des dieux, ce ne sont bien sûr pas des chars ordinaires. Vous faites la course à travers les cieux d'étoile en étoile. Votre objectif est d'être le premier à atteindre la plantation d'oliviers d'Alpha du Centaure et Héra a promis au gagnant une bouteille du fameux Doux Nectar d'Elysium. Pour un prix aussi prestigieux, vous êtes déterminé à sortir victorieux.

Mais même pour les dieux, il y a des règles. Vous ne pouvez pas voler directement vers Alpha du Centaure, sinon Zeus (qui a le char le plus rapide) serait nettement le gagnant. Chacun d'entre-vous dispose d'une carte de la galaxie vous indiquant entre quelles étoiles vous pouvez voler.

Pour rendre la course encore plus passionnante, certaines étoiles sont reliées par des trous de ver. Traverser un trou de ver vous permet en fait de remonter dans le temps. Héra a donné des instructions strictes à Zeus et celui-ci ne peut utiliser les trous de ver (étant à la tête de tous les dieux, il se doit d'avoir un handicap), mais le reste d'entre-vous est autorisé à les utiliser aussi souvent que vous le souhaitez.

Supposez que la course commence au temps 0. Si vous entrez dans un trou de ver au temps t minutes, alors vous atteignez l'autre extrémité au temps t/2 minutes. Comme les dieux n'ont toujours pas inventé les fractions, si t est un nombre impair, alors vous devez l'arrondir en dessous. Par exemple, si vous entrez dans un trou de ver au temps 10 minutes, vous en sortirez au temps 5 et si vous entrez dans un trou de ver au temps 15 minutes, vous en sortirez au temps 7.

Votre objectif est de définir votre parcours à travers les cieux pour qu'il vous permette d'arriver à la plantation d'oliviers d'Alpha du Centaure le plus tôt possible. Notez que vous pouvez passer par Alpha du Centaure plus d'une fois, i.e., vous êtes autorisé à passer par Alpha du Centaure à un temps donné, utiliser un ou plusieurs trous de ver et y retourner plus tôt dans le temps pour gagner la course.

• 1 <= N <= 100, où N est le nombre d'étoiles.

La deuxième ligne de l'entrée contiendra deux entiers S et F, séparés par un espace, où S est l'étoile à laquelle vous commencez la course et F est l'étoile à laquelle vous la terminez (i.e., Alpha Du Centaure). On vous garantit que 1 <= S,F <= N.

La troisième ligne de l'entrée contiendra un seul entier P, représentant le nombre de chemins ordinaires que vous êtes autorisés à prendre pour aller d'une étoile à l'autre. Chacune des P lignes suivantes décrit un chemin et contient trois entiers A, B et T séparés par des espaces, qui signifient que vous êtes autorisé à aller de l'étoile A à l'étoile B et que le voyage vous prendra exactement T minutes. On vous garantit que 1 <= A,B <= N, que A <> B et que 1 <= T <= 1000.

La ligne suivante de l'entrée contiendra un entier W représentant le nombre de trous de ver. Chacune des W lignes suivantes décrit un trou de ver et contient deux entiers A, B séparés par un espace, indiquant que le trou de ver vous transporte de l'étoile A à l'étoile B (et vous fait remonter dans le temps). On vous garantit que 1 <= A,B <= N et A <> B.

Notez que tous les chemins et trous de ver sont en sens unique. C'est à dire que si l'entrée contient un chemin ou trou de ver allant de l'étoile A à l'étoile B, vous ne pouvez pas utiliser ce chemin ou trou de ver pour aller de l'étoile B à l'étoile A (bien sûr, un autre chemin ou trou de ver allant de B à A peut apparaître autre-part dans l'entrée). On vous garantit que deux chemins ou trous de ver ne vous amèneront jamais de la même étoile A à la même étoile B et qu'il est toujours possible d'atteindre Alpha du Centaure.

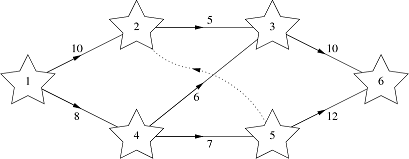
L'exemple d'entrée représente la carte illustrée ci-dessus. Les chemins normaux sont marqués comme des lignes continues et les trous de ver sont indiqués par des pointillés. Le départ de la course se fait sur l'étoile 1, sur la gauche et l'arrivée sur l'étoile 6, sur la droite.

La route la plus courte utilisant des chemins ordinaires du départ à l'arrivée est 1 -> 4 -> 3 -> 6, ce qui prend un temps total de 8+6+10=24 minutes. Cependant si l'on utilise le trou de ver, on peut atteindre l'arrivée plus tôt.

Si l'on voyage le long du chemin ordinaire 1 -> 4 -> 5, on atteint l'étoile 5 au temps 15. Emprunter le trou de ver 5 -> 2 nous ramène au temps 7 et l'on peut ensuite terminer le voyage par le chemin 2 -> 3 -> 6 pour atteindre l'arrivée au temps final de 7+5+10=22.