Pour la première fois depuis longtemps, sans doute à cause du changement climatique, il a beaucoup neigé dans votre région. Vous décidez d'en profiter pour organiser une compétition de luge dans les collines se trouvant derrière votre maison. Vous cherchez un endroit adapté pour y créer une piste, et souhaitez trouver une zone qui permette aux luges d'atteindre des vitesses élevées, bien qu'il n'y ait pas beaucoup de pentes raides dans les environs.

Vous avez obtenu une carte topographique de la zone, sur laquelle des contours sont représentés. Ces contours sont des cercles parfaits, et la carte indique l'altitude de la zone qui touche le bord intérieur de chaque cercle. La zone se trouvant en dehors de tous les cercles a une altitude de zéro. Comme ces contours sont la seule information dont vous disposez sur la forme des collines, vous pouvez considérer que les zones entre les contours sont plates. Deux contours ne se croisent jamais et ne se touchent jamais.

En utilisant cette carte, votre but est de trouver une piste qui ne traverse pas plus de K cercles, pour un nombre donné K (vous ne voulez pas que la piste soit trop bosselée), et telle que la différence totale d'altitude entre le point de départ et l'arrivée soit aussi grande que possible. Votre piste peut contenir des parties en montée mais ne doit jamais atteindre une altitude plus élevée que le point de départ.

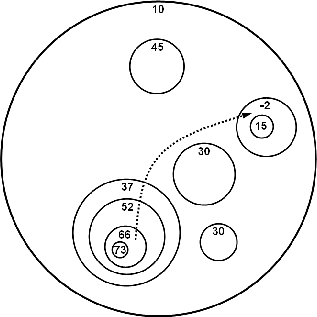
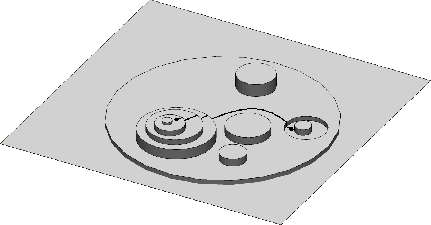
Par exemple, le diagramme ci-dessous montre une telle carte. Si le nombre maximum de cercles que vous pouvez traverser est K = 4, alors la piste ayant la plus grande différence d'altitude est celle représentée par la ligne pointillée, qui a une différence d'altitude de 66 - (-2) = 68. Le deuxième diagramme donne une vue plus claire du paysage décrit par cette carte (pas à l'échelle).

Pour 95% des points disponibles :

• 1 <= C <= 2 000, où C est le nombre de cercles sur la carte;
• 1 <= K <= 200, où K est le nombre maximal de cercles que votre piste peut croiser;
• -1 000 <= X,Y <= 1 000, où X et Y sont les coordonnées du centre d'un cercle;
• 1 <= R <= 2 000, où R est le rayon d'un cercle;
• -1 000 <= A <= 1 000, où A est l'altitude d'une zone.

Pour 30% de ces points (qui sont une partie des 95% mentionnés ci-dessus) :

• 1 <= C <= 100, où C est le nombre de cercles de la carte;

De plus, pour les 5% de points restants :

• 1 <= C <= 40 000, où C est le nombre de cercles de la carte.

Votre programme doit lire sur l'entrée standard. La première ligne de l'entrée doit contenir les entiers C et K, où C est le nombre de cercles de la carte, et K est le nombre maximal de cercles que votre piste peut traverser.

Les C lignes suivantes décrivent les cercles par ordre croissant de leur rayon. Chacune de ces lignes décrit un cercle sous la forme de quatre entiers séparés par des espaces : X_i, Y_i, R_i et A_i, où (X_i,Y_i) sont les coordonnées du centre du cercle, R_i est le rayon et A_i est l'altitude des zones qui touchent le bord interne du cercle..

Votre programme doit écrire une ligne sur la sortie standard. Cette ligne doit contenir un simple entier, qui donne la différence maximale d'altitude que vous pouvez obtenir entre le point de départ et l'arrivée d'une piste en respectant les contraintes décrites ci-dessus.