Pour des raisons encore inconnues, l'escalade en salle est en train de devenir un passe-temps populaire parmi de nombreux ex-philatélistes, philantropes et philosophes. Vous avez vous-mêmes decidé de suivre la tendance, et commencez à vous préparer à devenir le champion du monde d'escalade. L'escalade en salle consiste à aller du bas d'un mur au sommet en n'utilisant que votre force pour monter, et en faisant tout votre possible pour ne pas tomber. Près du sommet se trouve une cloche que vous sonnez pour faire part au monde de votre exploit.

Le mur est une surface plane à deux dimensions, contenant des prises en divers points. Pour s'accrocher au mur, vous devez être aggripé à trois prises distinctes quand vous êtes stables, ou à deux prises distinctes quand vous vous déplacez. Si vous en avez moins, vous tombez bêtement !

Pour vous déplacer sur le mur, vous pouvez lâcher l'une de ces trois prises, puis attraper une nouvelle prise. Le temps nécessaire pour effectuer ce déplacement est égal à la somme des distances horizontales et verticales entre la prise que vous avez lâchée, et celle que vous attrapez.

Comme vous ne pouvez atteindre qu'une certaine distance, chacune des trois prises auxquelles vous êtes agrippé doit être à au plus R mètres d'une autre prise que vous tenez, ceci mesuré par la somme des distances horizontales et verticales entre les deux points. Notez qu'elles n'ont pas à être toutes à R mètres les unes des autres. Par exemple, la configuration de départ du diagramme ci-dessous (représentée par les lignes pointillées) a une distance de 2 entre les points 1 et 2, une distance de 2 entre les points 2 et 4, mais une distance de 4 entre les points 1 est 4. Ceci est une configuration valide même si R = 2.

Pour devenir le grimpeur le plus rapide au monde, vous devez déterminer un ensemble de déplacements qui vous mènera à la cloche aussi vite que possible. La cloche est située sur l'une des prises (mais n'est pas nécessairement la plus haute prise). On vous indique sur quelles prises vous commencez à grimper, et on vous garantit que celles-ci correspondent à une situation valide.

Etant donné (i) l'ensemble des prises d'un mur décrites par des coordonnées (x,y) sur un plan et (ii) vos prises de départ, votre objectif est de trouver le temps le plus petit nécessaire pour aller de la position de départ à la cloche.

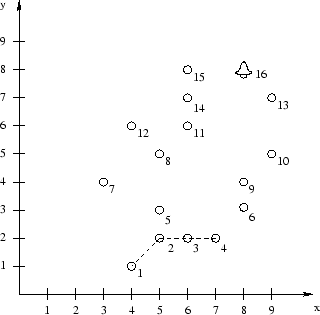
Par exemple, considérez le diagramme ci-dessus avec R = 2. Chaque cercle représente une prise. Il y a 16 prises (en comptant celle avec la cloche). Supposez que l'on vous demande de commencer agrippé aux prises 1, 2 et 4 comme indiqué. Une manière possible d'atteindre la cloche serait :

• lâcher la prise 4 et attrapper la prise 3 (1 seconde);
• lâcher la prise 1 et attrapper la prise 5 (3 secondes);
• lâcher la prise 2 et attrapper la prise 8 (3 secondes);
• lâcher la prise 3 et attrapper la prise 11 (4 secondes);
• lâcher la prise 5 et attrapper la prise 15 (6 secondes);
• lâcher la prise 8 et attrapper la prise 16 (6 secondes);

Ceci demande un total de 1+3+3+4+6+6 = 23 secondes, et est en fait le moyen le plus rapide d'atteindre la cloche.

• 1 <= N <= 50, où N est le nombre de prises sur le mur;
• 1 <= R <= 6, où R est la distance que vous pouvez atteindre (i.e. la somme maximale de la distance horizontale et verticale entre chaque point que vous tenez, et le point le plus proche que vous tenez);
• -1,000 <= x,y <= 1,000, où x et y sont les coordonnées d'une prise.

De plus, pour des tests correspondant à 50% des points, N <= 20.

Votre programme doit lire sur l'entrée standard. La première ligne de l'entrée contiendra les entiers N et R, séparés par un espace. Les N prises seront numérotées 1...N. La deuxième ligne contiendra les trois entiers distincts A, B et C qui indiquent les trois prises à partir desquelles vous commencez (1 <= A,B,C <= N).

Les N lignes suivantes décrivent les positions des prises. La ième de ces lignes décrit la position de la ième prise, par deux entiers x_i et y_i. Deux prises n'ont jamais la même position. La cloche est toujours attachée à la Nième prise.

Votre programme doit écrire une ligne sur la sortie standard.

Cette ligne doit contenir un simple entier, qui donne le temps le plus petit nécessaire pour aller de la position de départ à la cloche. On vous garantit qu'il sera toujours possible d'atteindre la cloche.

16 2
1 2 4
4 1
5 2
6 2
7 2
5 3
8 3
3 4
5 5
8 4
9 5
6 6
4 6
9 7
6 7
6 8
8 8

23