Vous êtes membre d'une équipe d'archéologues qui vient juste de découvrir une chambre secrète dans la grande pyramide de Gizeh. À votre grande déception, cette chambre est complètement vide, à part 22 petites pierres cubiques disposées en cercle sur le sol, au milieu de la chambre.

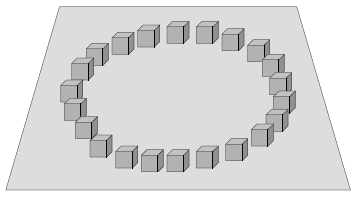
Vous remarquez que deux de ces cubes sont brisés, et après une observation plus approfondie, vous vous rendez compte qu'à l'intérieur de chacun d'eux, au milieu et parallèlement au sol, est gravé un hiéroglyphe. Un message caché du plus haut intérêt historique attend d'être découvert. Cependant, vous ne pouvez pas casser ni même déplacer les 20 cubes restants pour lire le message, donc vous décidez de recourir à la radiographie, en prenant des images aux rayons X de chaque cube.

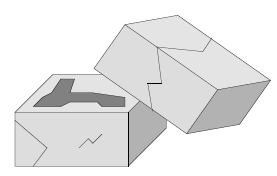
Les résultats montrent clairement que, comme vous vous y attendiez, un hiéroglyphe est gravé à l'intérieur de chaque cube, selon un plan parallèle au sol. Mais comme les radiographies sont prises à partir des côtés du cube et non du haut, vous ne pouvez pas lire le hiéroglyphe directement. Vous avez besoin de votre ordinateur pour vous y aider.

Pour chaque cube, la tranche sur laquelle est gravé le hiéroglyphe peut être représentée par une grille de NxN cases, chacune étant pleine ou vide. À partir de vos trois radiographies, vous connaissez le nombre exact de cases vides dans chaque colonne, ligne et diagonale (les diagonales sont dans la direction haut-gauche vers bas-droite). Les coordonnées des cases de la grille sont telles que la case du coin supérieur gauche a les coordonnées (0,0), et celle du coin inférieur droit les coordonnées (N-1,N-1). Les lignes, colonnes et diagonales sont numérotées 0,1,2,...

Une case de coordonnées (x,y) appartient à la colonne x, à la ligne y, et à la diagonale x - y + (N - 1); par conséquent, la petite diagonale du coin inférieur gauche est la diagonale 0, la longue diagonale passant par les cases (0,0) et (N-1,N-1) est la diagonale N-1, et la petite diagonale du coin supérieur-droit est la diagonale 2N-2.

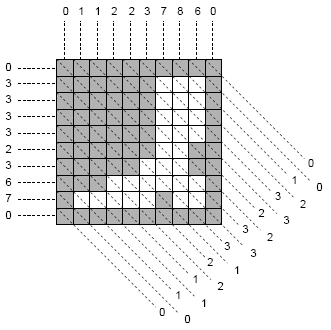
Le schéma ci-dessus est un exemple de hiéroglyphe avec le résultat des trois radiographies; il indique le nombre de cases vides dans chaque colonne, ligne et diagonale.

Étant donné le nombre de cases vides dans chaque colonne, ligne et diagonale de la grille, votre objectif est de trouver un hiéroglyphe dont le nombre de cases vides dans chaque direction est le plus proche possible de celui qui correspond dans l'entrée.

• 1 <= N <= 100, où N est la longueur du côté de la grille, en cases.

Votre programme doit lire sur l'entrée standard. La première ligne contiendra l'entier N, la taille de la grille NxN. La deuxième ligne contiendra N entiers séparés par des espaces. Le i^ème de ces entiers est le nombre de cases vides dans la i^ème colonne de la grille, en partant de la gauche. La troisième ligne contiendra N entiers séparés par des espaces. Le i^ème de ces entiers est le nombre de cases vides dans la i^ème ligne de la grille, en partant du haut. La quatrième ligne contiendra (2N - 1) entiers séparés par des espaces. Le i^ème de ces entiers est le nombre de cases vides dans la i^ème diagonale de la grille, en partant du coin inférieur gauche.

Votre programme doit écrire N lignes sur la sortie standard, décrivant un hiéroglyphe possible. Chaque ligne doit contenir N caractères décrivant une rangée de la grille, où le caractère '1' indique une case pleine, et '0' une case vide. La sortie ne doit pas contenir d'espace.

10
0 1 1 2 2 3 7 8 6 0
0 3 3 3 3 2 3 6 7 0
0 0 1 1 1 2 2 1 3 3 3 2 2 3 3 2 1 0 0

1111111111
1111110001
1111110001
1111110001
1111110001
1111110011
1111100011
1110000001
1000001001
1111111111

Score

Pour un test d'entrée donné, les nombres de cases vides sur chaque colonne, ligne et diagonale sont comparés aux valeurs d'entrée. L'erreur d'une colonne, ligne ou diagonale est la valeur absolue de la différence entre la valeur du test d'entrée et la valeur obtenue pour votre sortie. L'erreur totale de votre sortie sera la somme de ces erreurs. Votre score pour le test d'entrée sera:

• 0%, si l'erreur totale de votre sortie est supérieure à l'erreur totale obtenue avec une grille ne comportant aucune case vide;
• 100%, si l'erreur totale de votre sortie est de zéro;
• sinon, il sera déterminé selon une loi linéaire en fonction de l'erreur totale de votre sortie, les scores 0% et 100% sur l'échelle correspondant aux erreurs totales décrites ci-dessus.