Les Roues du Destin consistent en un jeu de W roues circulaires, placées l'une derrière l'autre comme illustré ci-dessous. Le contour de chaque roue est divisé en S segments identiques, dont certains sont percés d'un trou.

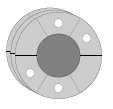
Votre voyante va vous demander de faire tourner chaque roue l'une après l'autre. Lorsque les roues s'arrêteront de tourner, elle cherchera des trous qui sont alignés sur toute la longueur, de l'avant à l'arrière (de telle sorte que vous puissiez voir au travers de l'ensemble des roues). Pour chaque ensemble de trous alignés, on vous garantit une année de prospérité et de code sans bug.

Heureusement, vous avez utilisé ce système de nombreuses fois, et êtes capables de faire tourner chaque roue exactement comme vous le souhaitez. Votre but est de décider jusqu'où faire tourner chaque roue, pour qu'un maximum de groupes de trous puisse être aligné.

Par exemple, considérez l'ensemble de W=3 roues illustré ci-dessous, chacun étant divisé en S=6 segments.

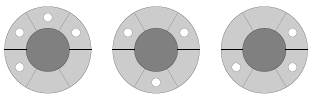
En faisant tourner la deuxième roue d'un segment dans le sens des aiguilles d'une montre, et en faisant tourner la troisième roue de deux segments dans ce même sens, vous pouvez placer les trois roues comme indiqué ci-dessous. Lorsque les roues sont placées l'une derrière l'autre, il y a deux ensembles de trous alignés sur toute la longueur, de l'avant à l'arrière. Ceci est illustré sur le dernier diagramme, du côté droit.

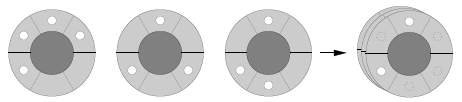
{On ne vous demande pas de donner la meilleure solution existante.}

Votre but est d'aligner autant de groupes de trous que possible. Votre programme va alors affronter d'autres programmes, les meilleures solutions obtenant plus de points.

• 1 <= W <= 50, où W est le nombre total de roues;
• 1 <= S <= 50, où S est le nombre total de segments divisant le contour de chaque roue.

De plus, 30% des points sont associés à des tests pour lesquels les segments satisfont S <= 20.

Les W lignes qui suivent décrivent chacune une roue. Chaque ligne contient S entiers séparés par des espaces, décrivant les segments de la roue dans l'ordre des aiguilles d'une montre, en commençant en haut. Pour chaque segment, l'entier 0 représente un trou dans la roue et l'entier 1 représente l'absence de trou.

Une fois que ces W lignes ont été écrites, votre programme doit écrire une ligne supplémentaire sur la sortie. Cette ligne doit contenir un seul entier : le nombre total de groupes de trous qui sont alignés sur toute la longueur, de l'avant à l'arrière.

Il n'y a pas de "meilleure solution" particulière, que l'on vous demande d'obtenir. Votre score sera en effet déterminé relativement aux solutions des autres candidats contre lesquels vous concourrez (ainsi que la solution des juges).

Une solution simple consiste à examiner chaque roue tour à tour du haut en bas, et à chaque étape, la faire tourner pour aligner autant de trous que possible avec toutes les roues au dessus d'elle. Une telle solution est définie comme obtenant 30% des points.

Pour chaque scénario d'entrée, le candidat qui aligne le plus de groupes de trous sera identifié. Supposons que ce candidat aligne H ensembles de trous au total.

Votre score pour ce scénario d'entrée sera alors :

• 100% si votre programme trouve une solution qui a également H groupes de trous alignés;
• 30% si votre programme trouve une solution égale à la solution simple décrite ci-dessus;
• 0% si votre programme génère une solution incorrecte (i.e., vous calculez incorrectement le nombre de groupes de trous qui sont alignés, ou vous ne suivez pas le format de sortie précisément);
• sinon, il sera déterminé selon une échelle linéaire, en fonction du nombre de groupes de trous que votre programme aligne, les scores de 100% et 30% sur l'échelle, correspondant aux solutions décrites ci-dessus.

Par exemple, considérez un scénario d'entrée pour lequel la solution simple aligne 26 groupes de trous. Si la meilleure solution trouvée par un candidat (ou les juges) aligne 40 ensembles de trous, alors l'échelle de score pour une solution correcte sera la suivante :