Trévor le singe a été placé dans une réserve animalière artificielle. Il apparait immédiatement que la forêt n'est pas naturelle : tous les arbres ont été plantés selon une grille parfaite, chaque arbre étant séparé d'1 mètre de ses voisins. Les arbres de cette forêt sont si proches les uns des autres, qu'aucune grosse branche ne peut pousser et par conséquent, Trévor n'a pas d'endroit tranquille où se reposer. Il résoud ce problème en construisant un certain nombre N de nids, placés sur certains arbres.

Les responsables de la réserve ont délimité le territoire de Trévor par un carré de S mètres de côté, situé bien à l'intérieur de la réserve. Tous les nids de Trévor se trouvent à l'intérieur de ce carré, ou sur sa frontière. Trévor est autorisé à sortir de son territoire, mais la réserve est si grande que même s'il le fait, il n'a aucune chance d'en atteindre les limites.

Comme toutes les branches sont petites, il est plutôt risqué pour un gros singe comme Trévor, de passer d'arbre en arbre. Pour cette raison, le seul moyen dont il dispose pour passer d'arbre en arbre est de se balancer grâce à des lianes, comme le lui a enseigné Tarzan dans sa jeunesse. Dans cette forêt, on trouve toujours des lianes facilement là où on en a besoin, ce qui en fait un moyen de transport rapide et efficace. Il y a cependant des restrictions :

• Pour pouvoir se balancer entre deux arbres, il ne doit y avoir aucun autre arbre le long de la ligne droite qui les relie (sinon, paf le singe).
• La longueur des lianes ne permet de se déplacer qu'à des distances de L ou moins, en un saut.

Sauter de liane en liane est fatiguant, même pour un singe bien entraîné, et Trévor souhaite minimiser sa fatigue quand il se déplace entre ses nids. Pour passer d'un nid à l'autre, il utilise des lianes d'arbre en arbre et peut se reposer sur d'autres nids le long du chemin. Comme ces pauses lui permettent de bien reprendre son souffle, Trévor ne mesure pas sa fatigue par le nombre total de sauts. Il mesure en fait sa fatigue par le plus grand nombre de sauts consécutifs qu'il doit effectuer à la suite sans se reposer.

Trévor est très fainéant et pas si intelligent : c'est un vrai singe. Il souhaite que vous l'aidiez à trouver un groupe d'au moins N/2 nids entre lesquels il peut se déplacer, de telle sorte que la plus grande fatigue qu'il doive endurer pour se déplacer entre toute paire de ces N/2 nids soit aussi petite que possible. Si N est impair, alors N/2 doit être arrondi à l'entier supérieur.

• 1 <= L <= 15, où L est la distance maximale pour un balancement.
• 2 <= S <= 200, où S est la longueur du côté du territoire de Trévor.
• 2 <= N <= 1000, où N est le nombre de nids que Trévor a construit.
• 0 <= Xi < S et 0 <= Yi < S, où (Xi, Yi) sont les coordonnées du ième nid.

De plus, dans 30% des jeux de tests, on vous garantit que L <= 3, S <= 100 et N <= 65.

La première ligne de l'entrée contient l'entier L, donnant la distance maximale qui peut être traversée en un seul saut (mesurée en mètres).

La deuxième ligne de l'entrée contient l'entier S, indiquant la longueur du côté du territoire carré (mesuré en mètres également).

La troisième ligne de l'entrée contient l'entier N, indiquant le nombre total de nids.

Chacune des N lignes suivantes contient deux entiers Xi et Yi séparées par un espace, donnant les coordonnées x et y de chaque nid. Deux nids ne se trouvent jamais sur le même arbre.

La sortie doit consister en une simple ligne contenant un entier : la fatigue minimale que Trévor doit endurer pour pouvoir se déplacer partout dans un groupe d'au moins N/2 nids.

3
6
5
0 0
0 3
5 1
5 5
1 5

2

Le jeu d'entrée ci-dessus décrit la forêt illustrée ci-dessous. Les arbres sont représentés par des disques noirs et les cinq nids sont indiqués par les lettres A, B, C, D et E. Notez que dans cet exemple, on peut se balancer à une distance maximale de L = 3 mètres.

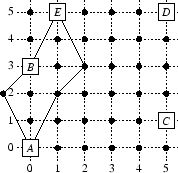
Considérez les nids A et B. Bien qu'ils soient à trois mètres d'écart, Trévor ne peut pas se balancer directement entre eux, car d'autres arbres sont sur le passage. Il doit donc effectuer au moins deux sauts. Par exemple, il peut se balancer de A=(0,0) à (-1,2), puis repartir vers B=(0,3). Ce chemin est représenté par un segment sur la carte. Notez que ce trajet sort du territoire de Trévor (ce qui est tout à fait autorisé).

Pour se déplacer entre les nids A et E, Trévor a besoin d'au moins trois sauts. Une fois de plus, il ne peut pas prendre un chemin plus direct, car des arbres sont dans le passage. Un chemin possible de A à E peut être de A=(0,0) à (1,2), puis vers (2,3) et finalement vers E=(1,5).

Remarquez que Trévor peut se déplacer de A à E avec une fatigue de seulement 2. Il peut le faire en allant de A à B en deux sauts, puis se reposer sur le nid B, et finalement passer de B à E avec un saut supplémentaire. Comme il effectue au plus deux balancements consécutifs sans se reposer, la fatigue totale pour ce déplacement de A à E est de 2.

Souvenez-vous que Trévor recherche un groupe de trois nids (N/2 arrondi au dessus) entre lesquels il puisse se déplacer. S'il choisit les nids A, B et E, on voit qu'il peut atteindre tout nid à partir de tout autre parmi ce groupe, avec une fatigue maximale de 2. Il n'y a pas d'autre groupe de trois nids qui donne un meilleur résultat (bien qu'il y ait de nombreux autres groupes qui donnent le même résultat), et 2 est donc la réponse finale.

Score

Le score pour chaque jeu d'entrée sera de 100% si la réponse correcte est fournie, et de 0% sinon.