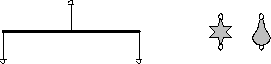
Des fils relient trois crochets à chaque tige. Celui du milieu permet d'accrocher l'ensemble de la tige sous un autre objet (soit le plafond, soit une décoration se trouvant plus haut). Une et une seule tige doit rattacher le mobile au plafond. Des deux côtés de chaque tige, des fils descendent et se terminent par un crochet. Ceci permet de suspendre une décoration sous chaque extrémité de la tige.

De nombreux types de décorations sont fournis, de différentes formes et poids. Deux anneaux sont fixés sur chaque décoration : l'un sur le dessus, l'autre en dessous. L'anneau du dessus peut être utilisé pour accrocher la décoration à un crochet se trouvant sous l'extrémité gauche ou droite d'une tige. L'anneau du dessous peut être utilisé pour y suspendre une autre tige.

Lorsque l'on construit un mobile avec ces éléments, aucun crochet ne doit être laissé libre, sauf celui du sommet, qui permet de suspendre l'ensemble du mobile au plafond. Tout autre crochet doit être attaché à une décoration. Les décorations n'ont pas autant de contraintes : certaines décorations peuvent avoir d'autres tiges qui y sont suspendues, d'autres peuvent ne rien avoir d'attaché à leur anneau inférieur. Une illustration d'un mobile complet est fournie ci-dessous. Les tiges sont numérotées de 1 à 7 et le poids de chaque décoration est indiqué à côté.

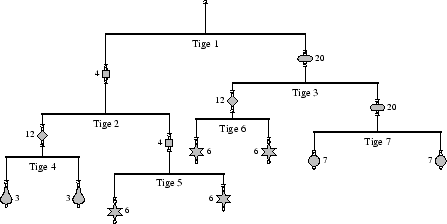
Votre petite soeur a terminé de construire un magnifique mobile, mais se plaint qu'il ne fonctionne pas ! En effet, le mobile est loin d'être bien équilibré : ce qui est suspendu d'un côté de certaines tiges est parfois bien plus lourd que ce qui est suspendu de l'autre côté.

Vous avez proposé votre aide, mais votre soeur se fâche lorsque vous lui expliquez que vous devrez déplacer certains éléments pour équilibrer le mobile. Elle ne veut pas que vous changiez quoi que ce soit à sa merveilleuse construction ! Le mobile est parfait ainsi, vous devez juste le faire marcher ! Vous finissez par la convaincre qu'il est nécessaire de changer quelque-chose pour améliorer l'équilibre, mais elle ne vous autorise à effectuer qu'une seule modification sur sa création.

Votre objectif est de rendre l'ensemble du mobile aussi équilibré que possible, en n'y apportant qu'une seule modification. Cette modification doit consister à détacher une tige de la décoration sous laquelle elle est suspendue, puis de l'attacher sous une autre décoration. Vous n'avez pas à vous inquiéter des possibilités de collisions entre les éléments du mobile lorsqu'il est mis en mouvement : vous pourrez toujours vous en occuper plus tard, en modifiant les longueurs de certains fils. Equilibrer le mobile est votre seule préoccupation.

Pour déterminer à quel point une tige donnée est équilibrée, vous devez calculer la valeur absolue de la différence entre le poids total suspendu sous chacune des deux extrémités de cette tige (une faible valeur est donc préférable). Pour évaluer l'équilibre de l'ensemble du mobile, vous devez faire la somme des différences obtenues pour toutes les tiges. Votre but est de réduire ce total à sa plus petite valeur possible en effectuant au maximum un changement. Notez que vous n'êtes pas obligé de faire un changement : vous pouvez choisir de ne rien modifier.

A noter également que lorsque vous déplacez une tige, vous ne pouvez pas l'attacher à une décoration à laquelle est déjà suspendue une tige. Les tiges, fils et crochets sont si légers qu'ils peuvent être considérés comme n'ayant pas de poids.

• 1 <= N <= 2000, où N est le nombre de tiges;
• 1 <= W <= 1000, où W est le poids d'une décoration.

De plus, dans 30% des jeux de tests, N <= 200.

Chacune des N lignes suivantes décrit une tige. Les tiges sont fournies dans l'ordre, de 1 à N (de telle sorte que la ligne 2 décrit la tige 1, et ainsi de suite). Chacune de ces lignes est de la forme W1 R1 W2 R2, où W1 et W2 sont les poids des décorations attachées directement sous les extrémités gauche et droites de la tige, et R1 et R2 sont les identifiants des tiges suspendues sous ces décorations (les tiges R1 et R2 sont suspendues respectivement sous les décorations de poids W1 et W2).

Si aucune tige n'est suspendue à une décoration, l'identifiant de tige correspondant sera zéro.

Dans l'exemple d'entrée, les différences de poids pour les tiges 1,...,7 sont respectivement 40, 2, 10, 0, 0, 0 et 0, ce qui donne une somme totale de 52. En déplaçant la tige 7 pour la placer sous l'une des décorations attachées à la tige 5, les différences de poids deviennent 12, 12, 4, 0, 14, 0 et 0, ce qui donne un total de 42. Aucune somme inférieure ne peut être obtenue sans déplacer plus d'une tige, donc 42 est la réponse finale.

Score :

Le score pour chaque jeu de test sera 100% si la bonne réponse est fournie sur la sortie, et 0% sinon.