Ces deux moines se partagent deux petits chalets, l'un en haut de la montagne, l'autre un peu plus bas. Pour éviter l'ennui, ils se sont mis d'accord pour s'échanger leur chalet une fois par mois. Le premier jour de chaque mois, ils partent chacun de leur côté exactement à la même heure et empruntent les petits sentiers de la montagne, pour se rendre à l'autre chalet. Ils doivent cependant s'assurer de ne pas se rencontrer et de rester dehors le moins longtemps possible, pour réduire les risques de tomber sur un éventuel randonneur.

Heureusement pour eux, de nombreux sentiers parcourent la montagne, ce qui leur offre de nombreuses manières de passer d'un chalet à l'autre. Chaque sentier relie deux croisements où peuvent se rejoindre plusieurs autres sentiers. Deux croisements reliés par un sentier ont toujours une altitude différente et chaque sentier ne fait que monter, ou que descendre entre ces croisements, suivant la direction dans laquelle on l'emprunte.

Les moines doivent consacrer un maximum d'énergie à la prière et souhaitent donc économiser leurs forces au maximum. Le moine qui descend ne doit ainsi jamais emprunter un sentier qui le force à monter et celui qui rejoint le sommet ne doit jamais redescendre pendant son trajet, car il devrait alors remonter d'autant ensuite.

Pendant leur parcours, les deux moines avancent à une vitesse toujours identique, d'exactement un mètre par seconde. Ils ont la possibilité de s'arrêter pour prier, mais le font toujours exactement au début d'une seconde et repartent au début d'une autre seconde. Leur temps d'arrêt doit être un multiple de 10 secondes, le temps de réciter un nombre entier de prières (chaque prière dure exactement 10 secondes).

Les sentiers ont tous une longueur multiple de 10 mètres. Un moine commence à marcher le long d'un sentier au début d'une seconde et atteint son autre extrémité exactement à la fin d'une seconde. Pour ne pas se croiser, les moines ne doivent donc jamais se trouver, au début d'une seconde, sur le même sentier ou à la même intersection.

Remarque : lorsqu'un moine se trouve exactement sur un croisement dont part un sentier, on ne considère pas qu'il se trouve sur ce sentier.

Vous devez écrire un programme qui détermine le temps total minimum nécessaire aux deux moines pour échanger leur chalet sans jamais se croiser. Le temps total est la somme du temps pris par chacun des moines pour son trajet, temps d'arrêts compris.

• 1 <= D <= 10, où D est le nombre de sentiers qui se rejoignent à un croisement donné.
• 3 <= C <= 10000, où C est le nombre de croisements.
• 2 <= S <= 20000, où S est le nombre de sentiers.
• 10 <= L <= 1000, où L est la longueur d'un sentier en mètres. L est multiple de 10.
• 0 <= A <= 1000, où A est l'altitude relative d'un croisement par rapport au chalet du bas, en mètres.

De plus, dans 50% des jeux de tests :

• 3 <= C <= 1000
• 1 <= S <= 2000

La deuxième ligne de l'entrée contient deux entiers séparés par un espace : l'identifiant du croisement correspondant au chalet du bas, suivi de celui du chalet du sommet.

Les C lignes suivantes contiennent chacune un entier : l'altitude d'un croisement. Les altitudes sont données dans l'ordre des identifiants des croisements. Ainsi, la 3ème ligne de l'entrée indique l'altitude du croisement d'identifiant 1.

Les S lignes suivantes décrivent les sentiers. Chaque ligne contient 3 entiers séparés par des espaces : les numéros des deux croisements reliés par le sentier, puis sa longueur L en mètres.

Attention : les croisements ne sont pas nécessairement fournis dans l'ordre de leur altitude. Le croisement K peut ainsi avoir une altitude plus élevée que le croisement K + 1. Les extrémités d'un sentier peuvent également être données dans l'ordre inverse de leurs altitudes.

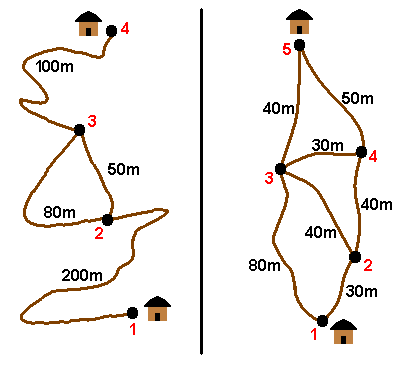
* illustration non contractuelle

Dans le premier exemple, le moine qui part du bas commence au croisement numéro 1. Il parcourt alors 200m sur le sentier 1 et arrive au temps 200 au croisement 2. Il parcourt ensuite 50m sur le sentier 2, vers le croisement 3, qu'il atteint au temps 250. Il emprunte finalement le sentier 4, qui va vers le chalet du sommet et parcourt 100m, pour l'atteindre au temps 350, soit après un trajet total de 5mn 40 secondes.

Le moine qui descend part de son chalet exactement au moment du départ du premier moine. Il parcourt tout d'abord 100m sur le sentier 4, pour arriver au croisement 3 au temps 100. Il emprunte alors le sentier 3, et parcourt 80m, mais fait une pause de 30 secondes pendant ce trajet, pour arriver au croisement 2 au temps 210, soit 10 secondes après le passage du premier moine, ce qui lui permet de ne pas le rencontrer. Il emprunte finalement le sentier 1 et atteint le chalet du bas au temps 410.

Le temps total de trajet des deux moines est donc de 350 + 410 = 760 secondes. Il leur est impossible d'échanger leur position en moins de temps.

Dans le deuxième exemple, le moine qui monte emprunte les sentiers 1, 3 et 6, pour atteindre le sommet après 110 secondes de marche sans pause. L'autre moine emprunte les sentiers 6, puis 2, et atteint le chalet du bas après 120 secondes de marche sans pause. Le temps total est donc de 230 secondes, ce qui est le plus petit temps possible.