France-IOI – Synthèse sur les structures de données (partie 1)

Ce document est une synthèse sur les structures de données de base vues jusqu'ici : table à accès direct, pile, file et tableau cumulatif 1D.

Outre un rappel des principes de chaque strucutre de données, un modèle de code est présenté pour chaque structure.

Surtout, les différentes utilisations classiques de chaque structure sont présentées. Ce dernier point ne doit pas être négligé : même si ces structures sont simples, penser à les utiliser lorsque c'est approprié peut être la clé de la résolution d'exercices nettement plus difficiles que ceux du niveau 1.

Table à accès direct

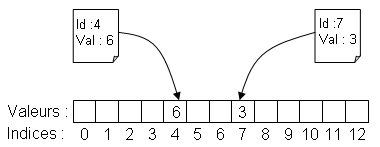
Une table à accès direct est un simple tableau tel que l'indice des cases du tableau correspond directement à un identifiant ou une propriété des objets que l'on manipule. Il permet d'accéder à des informations sur ces objets en O(1) à partir de leur identifiant ou de la propriété utilisée comme index.

Implémentation en Python

On considère un sujet où l'on dispose des tailles d'un certain nombre de personnes en mm, et on souhaite déterminer pour chaque taille, combien de personnes la possèdent. On va utiliser une table à accès direct indexée par la taille :

tailles = [lireTaille() for loop in range(MAX_NB_PERSONNES)]
nbOccurrences = [0] * (MAX_TAILLE + 1)
...
for personne in range(nbPersonnes):
   taille = tailles[personne]
   nbOccurrences[taille] = nbOccurrences[taille] + 1

Complexités :

L'insertion, la suppression ou la modification d'un élément se font en O(1). L'espace mémoire utilisé est de O(nbValeursPossibles).

Utilisation :

La table à accès direct peut être utilisée dès que l'on souhaite retrouver rapidement une information sur un objet à partir de son identifiant ou d'une de ses propriétés. La condition est que l'identifiant ou la propriété utilisée comme indice soit un entier compris dans un intervalle de taille raisonnable (en général, moins d'un million). Si l'intervalle de valeurs possibles est trop grand, on ne disposera pas d'assez de mémoire pour allouer le tableau.

On peut également utiliser des tables à accès direct à deux ou plus dimensions, pour accéder aux objets à partir de deux ou plus de leurs propriétés. L'intervalle de valeurs que l'on peut se permettre est alors nettement réduit.

On utilisera souvent une table à accès direct pour noter si l'on a déjà rencontré ou non chaque élément, ou bien pour stocker le nombre d'occurrences de chaque élément rencontré. Plus généralement, on peut l'utiliser pour associer toutes sortes de propriétés à chaque objet, et accéder rapidement à ces propriétés à partir de celles utilisées comme indice(s).

Cette utilisation correspond aux sujets lettre la plus présente et liste sans doublons

Pile

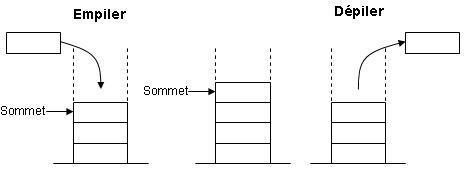
Une pile est un conteneur dans lequel on peut ajouter des objets, et retirer à tout moment le dernier objet ajouté parmi ceux restants. Il correspond à l'idée qu'on se fait d'une pile d'assiettes, où l'on ajoute des assiettes l'une après l'autre au sommet de la pile, et les retire également du sommet. Les opérations de base sont les suivantes, dont on donne les noms standards en anglais :

push : ajouter un objet au sommet de la pile
pop : retirer un objet du sommet de la pile
top : lire l'objet se trouvant au sommet de la pile
size : retourne le nombre d'objets de la pile.

On dit qu'il s'agit d'une structure LIFO, de l'anglais Last In, First Out : dernier entré, premier sorti.

Pour l'implémenter, en supposant que l'on connaît la capacité maximale nécessaire, on peut utiliser un simple tableau et un compteur du nombre d'objets dans le tableau.

Implémentation en Python

Une première implémentation naïve à l'aide d'un tableau.

pile = [None] * MAX_NB_OBJETS
nbObjets = 0

def push(objet):
   pile[nbObjets] = objet
   nbObjets = nbObjets + 1
   
def pop():
   nbObjets = nbObjets - 1
   return pile[nbObjets]
   
def top():
   return pile[nbObjets - 1]
   
def size():
   return nbObjets

Les tableaux en Python sont en fait des listes et ils peuvent être utilisés efficacement et naturellement pour représenter des piles :

Déclaration : pile = []
Empiler un objet : pile.append(objet)
Dépiler : sommet = pile.pop()
Lire le sommet : sommet = pile[-1] (les indices négatifs sont spécifiques à Python)
Obtenir le nombre d'éléments : len(pile)
Tester si la pile est vide : pile == [] ou len(pile) == 0

On peut aussi utiliser la structure deque() du module collections qui est aussi efficace et peut être aussi utilisée pour implémenter une file. Par contre il ne faut surtout pas utiliser LifoQueue() du module queue dont le temps d'accès peut être jusqu'à 10 fois supérieur et qui n'est pas prévu pour cela contrairement à ce que son nom pourrait laisser croire.

Complexités :

Les opérations push, pop, top et size ont une complexité en temps de O(1). La complexité en mémoire est de O(maxObjets).

Utilisations :

On peut distinguer quatre types d'utilisation de la structure de pile, qui couvrent à peu près tous les cas où cette structure est utilisée en pratique. Il est donc important de les retenir, et surtout de penser à utiliser une pile dès que l'on reconnaît une situation correspondant à l'un de ces cas.

Utiliser une pile comme simple conteneur
Si l'on souhaite un conteneur dans lequel on peut stocker des éléments, puis les en retirer sans se soucier de l'ordre dans lequel ils sont obtenus, utiliser une pile est la manière la plus simple d'implémenter un tel conteneur. On utilisera donc souvent une pile sans utiliser ses spécificités particulières, simplement parce que c'est le choix par défaut lorsqu'on a besoin d'un conteneur quelconque.
Utiliser deux piles pour gérer des insertions dans une liste parcourue élément par élément
Cet usage correspond au sujet Classeur.
Une première pile stocke tous les éléments à gauche de la position courante, et une deuxième pile stocke tous les éléments à droite de la position courante. On insère un élément en le plaçant dans la pile de droite.
Utiliser deux piles est plus simple et demande moins de mémoire qu'une liste doublement chaînée, qui oblige à stocker deux pointeurs pour chaque objet, sans compter l'espace supplémentaire lorsque les noeuds sont alloués dynamiquement.
Utiliser une pile pour stocker les objets plus grands que leurs suivants
Cet usage correspond au sujet Collage d'affiches.
On dispose ici d'un moyen de comparer les objets que l'on place sur la pile. Lorsque l'on ajoute un objet, avant de l'ajouter sur la pile, on va supprimer de celle-ci tous les objets qu'elle contient et qui sont plus petits que l'objet ajouté. Si l'on fait cela systématiquement, chaque objet de la pile est plus petit que tous ceux qui le précèdent, donc les objets restants dans la pile sont stockés par ordre décroissant, le plus petit étant au sommet de la pile. Lorsque l'on ajoute un nouvel objet, pour retirer tous ceux qui sont plus petits, il suffit alors de dépiler les objets, tant que l'objet au sommet est plus petit que notre nouvel objet.

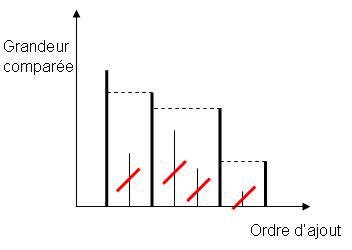
Pseudo-code de l'ajout d'objet pour cet usage :
```
   Ajouter(Objet obj)
      tant que ((!pile.empty()) && (pile.top() > obj)
         pile.pop()
      pile.push(obj)
```
Utiliser une pile est le moyen le plus simple et le plus efficace pour trouver, dans une liste d'objets, ceux qui sont plus petits que tous les précédents. Cet usage est relativement fréquent, avec un critère de comparaison entre éléments qui peut prendre toutes sortes de formes.
Utiliser une pile pour faire une récursion
Cet usage correspond entre autres aux sujets faisant appel à une exploration exhaustive, ou à un parcours en profondeur.
Remarque : lisez la description du principe de la pile d'appels si vous n'êtes pas très familiers avec son principe.
Lorsque l'on utilise une fonction récursive, la quantité de mémoire utilisée sur la pile d'appels augmente rapidement avec le nombre d'appels imbriqués, et il faut faire très attention à ne pas dépasser la limite de mémoire et obtenir un dépassement de pile, ou stack overflow en anglais. En effet, entre l'adresse de retour, les paramètres et les variables locales, on utilise plusieurs dizaines d'octets pour chaque niveau de récursion. De plus, l'espace réservé au stockage de la pile d'appels est souvent nettement inférieur à l'espace mémoire total disponible. Celui-ci dépend du système d'exploitation et de sa configuration, mais on a parfois une limite de 1Mo, et rarement plus de 16Mo disponibles.
Pour éviter ce problème, la solution consiste à se débarasser de la récursion, en utilisant sa propre pile. On réduit la mémoire utilisée, car on ne stocke dans la pile que le strict nécessaire et surtout, on n'est plus limité par l'espace mémoire réduit réservé à la pile d'appels.
Ce que l'on stocke en général dans cette pile, c'est une description de l'ensemble des étapes en cours de l'exploration. Dans le cas de l'exploration exhaustive et du parcours en profondeur, la pile va contenir la description du début du chemin en cours (les noeuds en cours de visite, dans l'ordre)

Principe de la pile d'appels

Dès que l'on utilise des fonctions dans un programme, on utilise indirectement une pile : la pile d'appels du système, qui est une zone de mémoire manipulée comme une pile et réservée à la gestion des fonctions. A chaque fois que l'on appelle une fonction, un certain nombre de données sont automatiquement empilées sur la pile d'appels, en commençant par l'adresse de retour de la fonction, c'est à dire un pointeur sur l'endroit du code auquel l'exécution devra revenir une fois l'exécution de la fonction terminée. Ensuite, l'ensemble des paramètres passés à la fonction est empilé, et enfin toutes les variables locales de la fonction sont également allouées sur cette pile. Au cours de l'exécution de la fonction, l'accès aux paramètres et aux variables locales se fait en calculant la position en mémoire de ces données, relativement à la position du sommet de la pile (on peut accéder aux objets sans avoir à dépiler les autres). Dès que la fonction se termine, toutes les variables locales et paramètres sont dépilées, l'adresse de retour est dépilée et utilisée pour reprendre l'exécution juste après l'endroit d'où la fonction a été appelée.

Une pile convient parfaitement à la gestion des données des fonctions, car les appels des diverses fonctions au sein d'un programme se font toujours de manière imbriquée : si l'on appelle une fonction A, au sein de laquelle on appelle une fonction B, on va commencer par empiler les données de la fonction A, puis appeler la fonction B et empiler ses données. On sort de la fonction B et dépile ses données, avant de sortir de la fonction A et de dépiler les données associées. L'ordre dans lequel les données sont réservées et libérées correspond donc bien à l'ordre de manipulation des données sur une pile.

Ce qui fait que l'on utilise une pile pour stocker les valeurs des paramètres et variables locales d'une fonction, plutôt que d'utiliser un endroit fixe en mémoire, c'est que la même fonction peut être appelée plusieurs fois simultanement : une fonction A peut appeler une fonction B, qui elle-même rappelle la fonction A, etc. Ou tout simplement, la fonction A peut se rappeler elle-même. On a alors une récursion. Comme on a plusieurs exécutions simultanées de la même fonction, on ne peut pas se contenter d'un seul endroit pour le stockage de ses paramètres et variables locales. La pile est donc indispensable dès que l'on a une récursion, pour que chaque exécution simultanée d'une fonction dispose de son propre espace de stockage des variables.

File

Une file est un conteneur dans lequel on peut ajouter des objets, et retirer à tout moment le premier objet ajouté parmi ceux restants. Il correspond à l'idée qu'on se fait d'une file d'attente, où les personnes qui arrivent se placent en queue de file, et attendent d'arriver en tête avant d'en sortir. Les opérations de base sont les suivantes, dont on donne les noms standards en anglais :

push : ajouter un objet en queue de la file
pop : retirer un objet de la tête de la file
front : lire l'objet se trouvant en tête de la file.
size : retourne le nombre d'objets de la file.

On dit qu'il s'agit d'une structure FIFO, de l'anglais First In, First Out : premier entré, premier sorti.

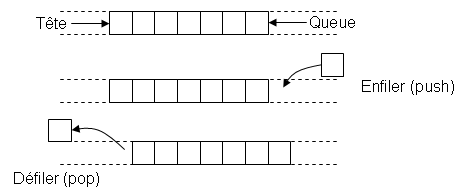
Pour l'implémenter, en supposant que l'on connaît la capacité maximale nécessaire, on peut utiliser ce que l'on appelle un buffer circulaire. On fait comme si l'on disposait d'un tableau de taille infinie, dans lequel on stocke les éléments de la file, entre une position de tête et une position de queue. La tête et la queue avancent le long du tableau au fur et à mesure de l'utilisation. On se ramène à un tableau de taille fixe en fixant la taille du tableau à une valeur plus grande que le nombre maximum d'éléments que contiendra la file, et faisant un modulo de cette valeur, sur les positions de tête et de queue à chaque accès. En pratique, on utilisera souvent une puissance de deux comme taille du tableau, pour pouvoir implémenter les modulos par de simples ET binaires.

Implémentation en C++

Cette implémentation est spécifique à un type d'objet donné. On le nommera ici Objet, que l'on remplacera par le type souhaité, suivant le besoin.

   NB_CASES_BUFFER = (1 << log2(MAX_NB_OBJETS))
   MASQUE = (1 << log2(MAX_NB_OBJETS))-1
   Objet file[NB_CASES_BUFFER];
   int tete = 0;
   int queue = 0;

   Objet& File(int index)
   {
      return file[index & MASQUE];
   }

   void Push(Objet obj)
   {
      File(queue & MASQUE) = obj;
      queue++;
   }

   Objet Pop()
   {
      tete++;
      return File(tete - 1);
   }

   Objet Top()
   {
      return File(tete);
   }

   int Size()
   {
      return queue-tete;
   }

La STL contient une implémentation générique de file, que l'on peut utiliser directement : queue. Voici les six points à connaître pour pouvoir l'utiliser :

Fichier à inclure : #include <queue>
Déclaration : queue<int> file; (on peut remplacer int par le type de son choix).
Enfiler un entier : file.push(42);.
Défiler : file.pop(); (retire l'objet de tête mais ne le retourne pas
Lire l'objet de tête : int tete = file.front();.
Obtenir le nombre d'éléments : file.size();.
Tester si la pile est vide : file.empty();.

Complexités :

Les opérations push_back, pop_front, front et size ont une complexité en temps de O(1). La complexité en mémoire est de O(maxObjets).

Utilisations :

La file est relativement peu utilisée en algorithmique. On peut cependant en noter les deux utilisations les plus classiques :

Maintenir le contenu d'une fenêtre glissante

Cet usage correspond au sujet Coup du siècle.

La file peut être utile pour stocker le contenu d'une fenêtre évoluant parmi des données, si jamais on ne dispose pas d'assez de mémoire pour stocker l'ensemble des données.

Lister des objets à traiter plus tard, dans l'ordre dans lequel on les découvre

Cet usage correspond à l'utilisation d'une file dans un parcours en largeur.

Lorsque l'on traite un objet, on découvre ses voisins, qui peuvent constituer des objets à traiter plus tard, dans l'ordre dans lequel on les a découverts. On les ajoute donc en queue de file.

Tableau cumulatif

Un tableau cumulatif est une structure permettant de répondre rapidement à certains types de questions portant sur les données contenues au sein d'intervalles de positions d'un tableau. L'exemple le plus classique concerne des questions de la forme : "quelle est la somme des valeurs se trouvant dans tel intervalle de positions du tableau ?".

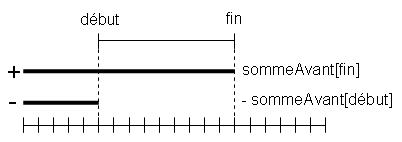
L'idée est de précalculer dans un tableau (le tableau cumulatif), toutes les réponses à la question pour les intervalles commençant au début du tableau. Tout intervalle [A,B[ peut être considéré comme une soustraction d'intervalles : [A,B[ = [0,B[ - [0,A[. Pour calculer la réponse à une question sur un intervalle [A,B[, on fait donc la différence entre les réponses aux questions sur les intervalles [0,B[ et [0,A[, que l'on a précalculées.

Implémentation en C++

A une position donnée du tableau cumulatif, on va stocker la somme des valeurs se trouvant avant la position corresponante du tableau de données. Pour rendre ce choix clair, on choisira un nom explicite pour le tableau, tel que sommeAvant.

int valeurs[MAX_NB_VALEURS];
int nbValeurs;
int sommeAvant[MAX_NB_VALEURS + 1]; // initialisé à 0

void RemplitCumulatif()
{
   sommeAvant[0] = 0;
   int somme = 0;
   for (int pos = 0; pos < nbValeurs; pos++)
   {
      somme += valeurs[pos];
      sommeAvant[pos + 1] = somme;
   }
}

int SommeEntre(debut, fin) // fin exclue
{
   return sommeAvant[fin] - sommeAvant[debut];
}

Le code de remplissage donné ici est écrit pour qu'il soit le plus clair possible. Le tableau cumulatif étant une structure que l'on utilise souvent, donc que l'on peut apprendre par coeur, on peut s'autoriser du code légèrement moins clair, mais plus court :

void RemplitCumulatif()
{
   sommeAvant[0] = 0;
   for (int pos = 0; pos < nbValeurs; pos++)
      sommeAvant[pos + 1] = sommeAvant[pos] + valeurs[pos];
}

Complexités :

La complexité se décompose en deux parties : le précalcul qui est effectué en O(nbValeurs), et le calcul pour chaque requête qui est effectué en temps constant, donc O(1).

On remarque que si l'on souhaite modifier ne serait-ce qu'une case du tableau de valeurs, toutes les cases qui suivent cette position dans le tableau cumulatif sont à mettre à jour. On peut donc considérer que la modification d'une valeur, lorsque l'on utilise un tableau cumulatif, est en O(nbValeurs).

La complexité en mémoire est de O(nbValeurs).

Utilisations

Le tableau cumulatif n'est utilisé que comme une structure permettant de répondre rapidement à des requêtes portant sur des intervalles d'un tableau de données, celui-ci n'étant jamais (ou rarement) modifié.

Le principe n'est cependant pas limité au cas où l'on demande une somme de valeurs : on peut l'utiliser pour tout type d'opération pour lequel une opération inverse existe : la soustraction est l'opération inverse de l'addition, la division est l'opération inverse de la multiplication, etc. On peut ainsi utiliser un tableau cumulatif pour des requêtes demandant le produit des valeurs au sein d'un intervalle de positions, avec la restriction que toutes les valeurs doivent être strictement positives (pour éviter d'obtenir des divisions par zéro).

Remarquez que dans le cas où l'on fait un cumulatif de type somme, on peut poser des questions de type "est-ce que cette zone contient un objet au moins", et pas seulement des questions sur le nombre total.

Pensez à vous inscrire pour valider les cours et résoudre les exercices.