Introduction

Il est impossible pour les ordinateurs de représenter de manière exacte l'ensemble des nombres décimaux (impossible pour un irrationnel par exemple) et en pratique il est même impossible de représenter tous les rationnels (cela prendrait trop de place en mémoire).

Aussi, on travaille généralement avec des décimaux connus à une certaine précision, en "oubliant" certains chiffres significatifs. Cette approximation peut naturellement conduire à des erreurs de calculs dans certains algorithmes numériques et l'objet de de cours est de vous donner un aperçu de ce phénomène et de vous montrer comment l'identifier dans des cas simples.

Représentation des décimaux

Ces informations sont tirées de cette page wikipédia, et présentées ici dans une version simplifiée.

Un décimal $valeur$ est représenté au sein d'un ordinateur sous la forme d'un triplet $$ (signe, mantisse, exposant) $$ tels que $$ valeur = signe \times (1.mantisse) \times 2^{exposant} $$

Il existe des types différents de décimaux, qui permettent d'avoir une précision différente, généralement :

• la "simple précision", codée sur 32 bits (1 de signe, 8 d'exposant et 23 de mantisse), permet d'avoir des décimaux avec 7 chiffres significatifs,
• la "double précision", codée sur 64 bits (1 de signe, 11 d'exposant et 52 de mantisse), permet d'avoir des décimaux avec 16 chiffres significatifs.

Ainsi, il est conseillé de toujours utiliser la double précision afin de faire des calculs précis, sachant qu'ils seront légèrement plus lent qu'avec des décimaux en simple précision.

Somme harmonique

Nous allons nous intéresser au calcul de la valeur de $$ u_n = 1 + \dfrac{1}{1} + \dfrac{1}{2} + \ldots + \dfrac{1}{n-1} + \dfrac{1}{n} $$ car l'on sait que $$ \lim_{n\mapsto\infty} u_n - ln(n) = \gamma $$ avec $\gamma$ la constante d'euler.

On va donc s'intéresser à la valeur de $$ P(n) = \left| u_n - ln(n) - \gamma \right| $$ qui devrait tendre vers 0 quand $n$ croît, et afficher sa courbe selon plusieurs méthodes de calculs différentes.

Algorithme naturel (en simple précision)

On considère l'algorithme suivant :

somme <- 0.0
Pour i allant de 1 à n 
   somme <- somme + 1 / i
Afficher ValeurAbsolue(somme - log(n) - gamma)

Si on représente la résultat, en échelle logarithmique, cela donne ceci

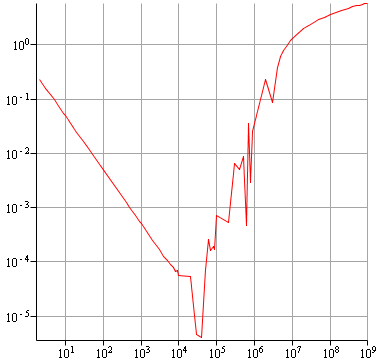
On voit donc que cela commence bien (la ligne droite du début) et que la précision augmente en fonction de $n$, mais vers $n=10000$ on commence à perdre de la précision, jusqu'à ce que cela soit catastrophique.

En pratique, comme la mantisse d'un nombre décimal à une précision finie, on va toujours perdre de l'information quand on va sommer un grand décimal et un petit, on va perdre au passage les derniers chiffres du petit décimal. Ainsi, le code suivant

x <- (10^20 + 0.1) - (10^20)
Afficher x

affichera la valeur 0.0 !

Algorithme inversé (en simple précision)

Pour essayer de minimiser les cas où on ajoute un petit décimal à un grand décimal, on peut essayer de sommer les valeurs en partant de la plus petite, avec l'algorithme suivant :

somme <- 0.0
Pour i allant de n à 1 
   somme <- somme + 1 / i
Afficher ValeurAbsolue(somme - log(n) - gamma)

Voilà le résultat obtenu :

C'est mieux mais toujours pas parfait, on a toujours une remontée rapide vers la fin.

Algorithme "diviser pour régner" (en simple précision)

Le principe est de d'abord sommer la première moitié de la somme, puis la seconde et d'additionner les deux valeurs. On fait bien sur cette opération de manière récursive, ce qui donne l'algorithme suivant :

fonction calculeRecursif(debut, fin)
   Si debut = fin
      Renvoyer 1 / deb
   Renvoyer calculeRecursif(debut, (debut + fin) / 2) 
          + calculeRecursif((debut + fin) / 2 + 1, fin)

somme <- calculeRecursif(1, n)
Afficher ValeurAbsolue(somme - log(n) - gamma)

Voilà le résultat obtenu :

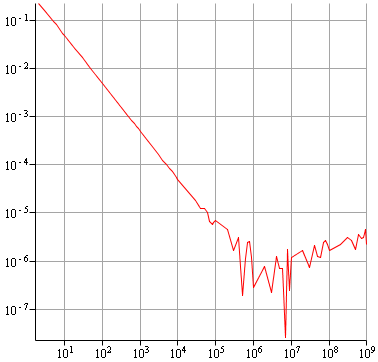
On commence à remonter un peu plus tard, mais surtout beaucoup moins vite, le résultat reste "pas trop mauvais".

Algorithme de Kahan (en simple précision)

L'idée de cet algorithme est de mesurer la perte de précision due aux additions faites et de la prendre en compte pour contrebalancer le calcul en conséquence à l'étape d'après. Il s'explique bien avec le code :

somme <- 0.0
compensationErreurs <- 0.0
Pour i allant de 1 à n
   valeurAAjouter <- 1 / i - compensationErreurs
   // Somme est grand, valeurAAjouter petit, on perd les derniers
   // chiffres de valeurAAjouter 
   sommeTemporaire <- somme + valeurAAjouter 
   // On récupère les premiers chiffres de valeurAAjouter
   compensationErreurs <- (sommeTemporaire - somme)
   // On récupère l'opposé des derniers chiffres de valeurAAjouter
   compensationErreurs <- compensationErreurs  - valeurAAjouter 
   somme <- sommeTemporaire

Afficher ValeurAbsolue(somme - log(n) - gamma)

Voilà le résultat obtenu :

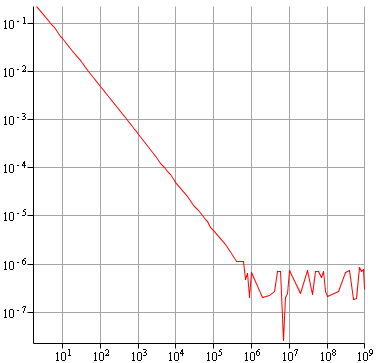
Non seulement on ne commence à remonter que vers $n=10^{-6}$, mais on reste ensuite toujours sous $10^{-6}$, on ne remonte pas vraiment. On garde donc une précision tout à fait correcte, et même très bonne, sachant qu'avec des décimaux en simple précision, on ne peut guère espérer descendre en dessous de $10^{-7}$ étant donné qu'on ne peut avoir que 7 chiffres significatifs.

Avec des décimaux en double précision

Si on lance les même algorithmes, mais avec des décimaux en double précision, voici ce qu'on obtient:

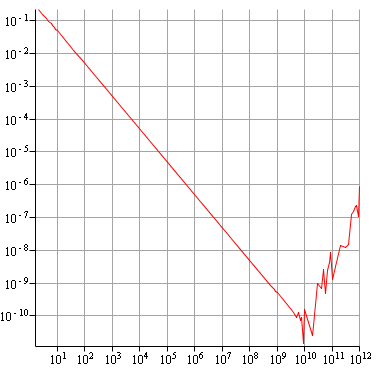
Algorithme naturel : diverge vers 10 milliards.

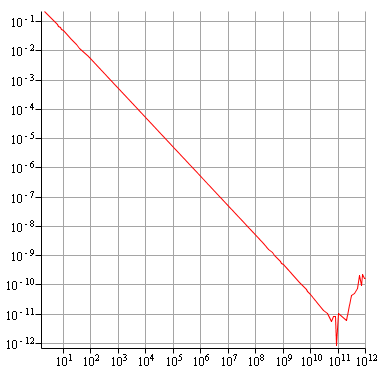
Algorithme inversé : diverge vers 100 milliards.

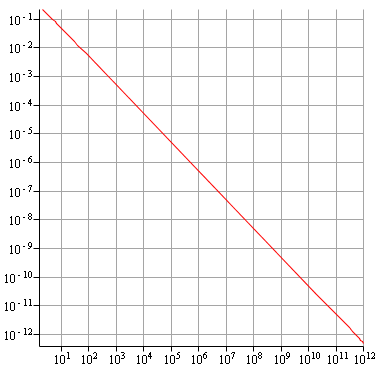
Algorithme "diviser pour régner" : ne diverge pas avant 1000 milliards.

Algorithme de Kahan : ne diverge pas avant 1000 milliards.

Même pour l'algorithme naturel, on a tout de suite une très bonne précision, car on a arrive à avoir une précision de $10^{-10}$ avant de constater une remontée. Quand aux deux derniers algorithmes, on a toujours la convergence même après $10^{12}$ itérations !

Utiliser des décimaux en double précision donne donc de très bons résultats, pour un effort quasi-nul.

Un exemple de non-convergence (en double précision)

Cet exemple est tiré d'un sujet du Bac 2012, et considère la suite d'intégrale $(I_n)$ définie pour tout $n$ entier naturel non nul par $$ I_n = \int_{0}^{1}x^ne^{x^2}\, dx. $$ et pour laquelle on peut montrer que $$ I_{n+2} = \frac{1}{2}e - \frac{n+1}{2}I_n. $$ et que $(I_n)$ est positive, décroissante et donc convergente.

Afin d'expérimenter un peu, on se propose de calculer certains termes de la suite avec l'algorithme suivant :

n <- LireEntier()
valeurInt <- 1 / 2 * e - 1 / 2 // Valeur de I_1
TantQue n <= 50
   valeurInt  <- 1 / 2 * e - (n + 1) / 2 * valeurInt
   n <- n + 2
Afficher valeurInt 

Si on affiche le graphe de la différence entre les valeurs données par cet algorithme, et les vraies valeurs pour $(I_n)$ on aura ceci, en échelle linéaire :

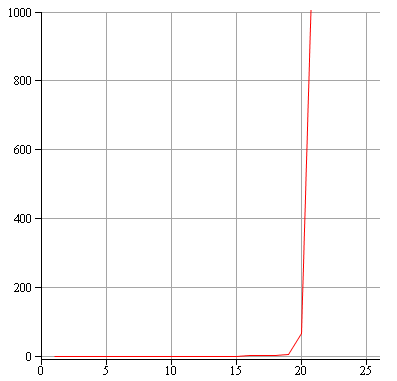
On est donc très proche de la bonne valeur au début et vers l'itérations 17 ou 18 rien ne va plus ! Pour voir ce qui se passe ensuite, il faut passer en échelle logarithmique :

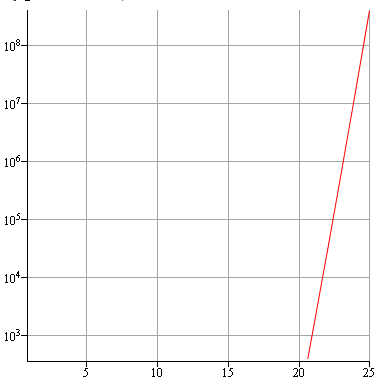
On arrive donc à quelque chose d'extrêmement mauvais et la suite de valeurs donnée par l'algorithme n'est ni positive, ni décroissante et encore moins convergente !

L'origine du problème est dans le facteur $(n+1)$ qui va faire "remonter" les mauvaises décimales de $(I_n)$ (celles, au delà de la 17ème, qui ne sont pas conservées en double précision). Dès que ces mauvaises décimales ont trop remontées, le calcul dérape fortement.

Conclusion

1. Toujours utiliser des décimaux en double précision ce qui évitera de nombreuses erreurs, sans demander de temps supplémentaire pour programmer des algorithmes "intelligents" pour sommer des valeurs.
2. Toujours représenter l'évolution de la précision en fonction de $n$ (ou du nombre d'itérations, selon le cas) et voir quel graphe on obtient. On peut ainsi facilement détecter des algorithmes instables quand ce qu'on voit ne correspond pas aux résultats théoriques qu'on sait démontrer (décroissance, convergence...)
3. La vitesse des ordinateurs actuels leur permet d'effectuer plus de 1 million d'itérations par seconde et permettent donc d'expérimenter très facilement la stabilité d'un algorithme. Il faut donc faire attention, en particulier dans des sujets d'examens (a fortiori du Bac), ne ne pas présenter des algorithmes qui "dérapent" au bout de quelques itérations. En cherchant à l'essayer en pratique, les élèves peuvent être perturbés par les résultats incohérents obtenus, l'explication de ce "dérapage" leur étant la plupart du temps hors de portée.