Méthode de recherche d'un algorithme

Mathias Hiron pour www.france-ioi.org

Voici un ensemble de conseils à appliquer pour trouver la solution d'un problème algorithmique, en particulier pour les problèmes du type de ceux proposés aux IOI. Prenez l'habitude de les appliquer sur tous les sujets, dans l'ordre, jusqu'à ce que cela devienne un automatisme. Une liste résumée de ces conseils est donnée en bas de la page.

Cette méthode est le fruit de plusieurs années d'expérience et s'améliore régulièrement, entre autres grâce aux réactions de nombreux candidats qui l'utilisent. Elle est issue de l'application d'une règle simple que nous vous conseillons de suivre : après avoir résolu un problème, prenez du recul sur votre processus de réflexion, et déterminez ce qui vous a permis d'avoir la bonne idée, ce qui vous a fait gagner du temps, ou ce qui vous en a fait perdre. Déduisez-en ce que vous pourrez faire à l'avenir pour être plus efficace et notez-le. C'est l'application de cette philosophie à nous-mêmes et aux candidats, qui a abouti à la méthode présentée ici.

Son premier objectif est de vous aider à réfléchir, sans rester coincé devant le problème : lorsque vous n'avez pas d'idée tout de suite, rester devant le problème en laissant libre cours à votre réflexion devient très vite une perte de temps. Ces conseils permettent d'avoir toujours de quoi avancer. Il ne s'agit pas d'une méthode miracle qui résout les problèmes à votre place, mais une fois que vous la maîtriserez, elle vous permettra très probablement d'obtenir de bien meilleurs résultats que si vous vous contentez de réfléchir sans méthode particulière.

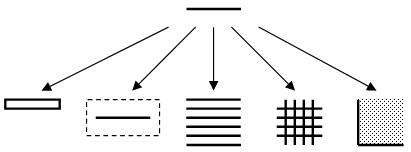
L'illustration suivante résume le fonctionnement de la méthode. Sans méthode particulière, votre intelligence, vos connaissances, etc. vous permettent déjà de résoudre des problèmes d'une certaines difficulté.

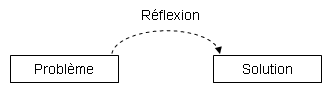
Appliquer une méthode revient à décomposer la réflexion en étapes, à poser des jalons qui vous permettent de résoudre des problèmes bien plus difficiles que ceux que vous êtes capable de résoudre naturellement.

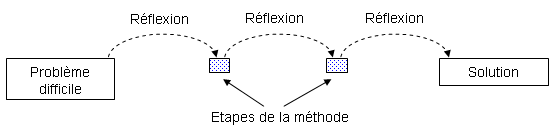
Après l'avoir appliquée systématiquement et entièrement de nombreuses fois, il est bien sûr possible que certaines parties ne vous conviennent pas, et que vous trouviez plus efficace de procéder autrement. Dans ce cas, n'hésitez pas à nous contacter, pour nous dire de quelle manière vous procédez, cela peut nous aider à améliorer ces conseils. Évitez cependant de décréter que certaines choses sont inutiles, avant même de les avoir mises plusieurs fois en pratique.

1) Lisez bien le sujet et reformulez-le

La première chose à faire consiste à bien lire le sujet, et entièrement.

Cela peut paraître évident, mais l'expérience montre qu'il arrive à tout le monde de lire le sujet un peu vite, et de ne pas voir certains détails importants. Pour éviter cela, il faut donc prendre son temps pour lire le sujet, et ne pas hésiter à le relire plusieurs fois pour bien tout comprendre et voir tous les détails.

Les problèmes vous sont généralement donnés sous la forme d'une petite histoire. Une partie de votre travail consiste à décrypter cette histoire pour vous faire une idée claire du problème. Souvent, l'essence du sujet peut se résumer en une ou deux phrases simples. Écrire ces phrases aide à mieux avoir l'ensemble du problème en tête, donc à le résoudre. Reformulez-donc le sujet le plus simplement possible, sous la forme d'une question. Relisez ensuite le sujet pour bien vérifier que votre reformulation est correcte, et qu'il n'y manque rien d'important.

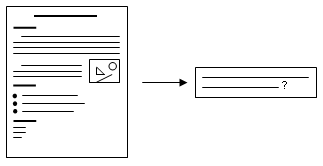
N'essayez pas de commencer à chercher des idées d'algorithmes au cours de la lecture, consacrez-vous entièrement à la compréhension du sujet. Si malgré cela vous avez une idée d'algorithme au cours de la lecture du sujet, vous pouvez la noter brièvement pour ne pas l'oublier, mais reprenez aussitôt la lecture sans y repenser. En cours de lecture, n'hésitez pas à noter les points importants et à souligner les détails à ne pas oublier.

Après cette phase de lecture, vous devez connaître le sujet suffisamment pour ne plus avoir le moindre doute et pouvoir rechercher un algorithme sans hésiter sur la nature du sujet.

2) Faites la liste des dimensions du sujet

Dans tous les sujets, on vous fournit un certain nombre de données en entrée, à partir desquelles vous devez calculer puis afficher un résultat. Ces données étant au cœur du problème, il est important de les décrire précisément et d'avoir bien en tête les valeurs qu'elles peuvent prendre. Chaque type d'information que l'on vous donne en entrée, ou que l'on vous demande en sortie, est ce que nous appellerons une dimension du problème.

Un moyen simple de déterminer quelles sont les dimensions associées à certaines données consiste à se demander quelles structures il est nécessaire de déclarer pour les stocker. Chaque variable ou attribut d'une structure simple est une dimension. L'indice d'un tableau 1D correspond également à une dimension, de même que chacune des valeurs contenues dans une case du tableau. Pour un tableau 2D, on a deux dimensions pour les indices, etc.

Juste après la lecture du sujet, notez donc bien clairement la liste de ses dimensions, en distinguant :

• Les dimensions d'entrée : elles correspondent à tout ce qui est fourni à votre programme.

• Les dimensions de sortie : elles correspondent à ce que l'on demande à votre programme d'afficher, ainsi qu'à ce qu'il est indispensable de calculer pour pouvoir obtenir le résultat. Par exemple, si on vous demande d'afficher le coût total d'un chemin, ce coût est une dimension de sortie, mais le nombre d'étapes du chemin correspondant l'est également, même si on ne vous demande pas de l'afficher.

• Les dimensions implicites : elles correspondent à des dimensions qui n'apparaissent que si l'on change de point de vue sur le sujet. Par exemple, si l'on vous donne des coordonnées de points dans le plan, l'angle des droites allant de chaque point à l'origine peut être vu comme une dimension (si cela semble utile) même s'il n'en est pas fait mention dans le sujet. De même, si l'on donne dans le sujet des rectangles sous la forme des coordonnées de deux sommets, il peut être intéressant de lister la largeur et la hauteur des rectangles comme dimensions implicites.

Pour chacune de ces dimensions, précisez :

• Les valeurs minimale et maximale. Elles sont souvent données directement dans le sujet, mais il est parfois nécessaire de faire un calcul pour les trouver, en particulier pour les dimensions de sortie.

  Les valeurs minimale et maximale de chaque dimension sont une donnée très importante du sujet. Le temps d'exécution et la quantité de mémoire nécessitées par votre programme en dépendent directement. Pour que votre programme obtienne un bon score, il faut donc qu'il fonctionne dans les limites imparties, même pour les valeurs les plus grandes de toutes les dimensions.

• Si l'ordre est important ou non pour cette dimension. Par exemple, s'il s'agit d'un indice de tableau, la solution change-t-elle si on change l'ordre des cases ?

  Si l'ordre des valeurs d'une dimension est important, alors vous pouvez envisager de vous baser dessus dans votre algorithme, par exemple en parcourant les données selon cet ordre. Si au contraire elles n'influencent pas le résultat, alors vous pouvez envisager d'imposer l'ordre de votre choix.

En dessous des dimensions, notez également les contraintes de temps et de mémoire du sujet. Ces contraintes ne sont pas définies au hasard : elles sont souvent choisies de telle sorte que l'algorithme le plus efficace puisse tout juste s'exécuter dans les limites imparties.

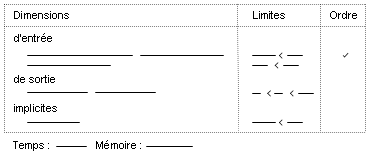
En regardant les dimensions et en les mettant en relation avec les limites de temps et de mémoire, vous pouvez déjà vous faire une bonne idée de la complexité en temps et mémoire que vous pouvez vous permettre. Pensez donc systématiquement à calculer ces complexités possibles, puis à partir de ces complexités, essayez de deviner le type d'algorithme à utiliser. Par exemple, si une complexité en temps de O(N · log(N)) semble le maximum possible d'après les limites, il y a de fortes chances que la solution fasse intervenir un algorithme de tri, une dichotomie, ou bien un arbre binaire.

3) Cherchez une bonne représentation visuelle du problème

L'un des moyens les plus efficaces pour avoir des idées sur un problème est, comme indiqué à l'étape suivante, de créer vos propres exemples, puis d'essayer de les résoudre à la main. Pour que cette étape soit efficace, il faut que l'on puisse « voir » un maximum de choses sur ces exemples.

Il existe souvent de nombreuses manières de les représenter, et suivant celle que vous choisissez, ce qu'il faut faire apparaît plus ou moins nettement. Choisir la ou les bonnes représentations visuelles est donc une étape cruciale dans la résolution d'un problème. Ce qui n'est pas du tout évident quand on lit la description d'un problème peut apparaître très nettement une fois celui-ci présenté selon une bonne représentation visuelle.

La représentation visuelle la plus intéressante n'est pas toujours celle qui semble naturelle au départ. Ne vous contentez donc pas de votre première idée, même si elle vous semble bonne. Dans certains problèmes, il y a de très nombreuses représentations visuelles intéressantes, mais un petit nombre d'entre elles, voire une seule fait apparaître l'idée de la solution.

Pour représenter un exemple du problème, vous ne disposez que d'une feuille de papier. Cette feuille n'a que deux dimensions, ce qui signifie que seules deux dimensions du problème pourront être représentées très clairement, et que les autres, quelle que soit la manière dont on les représente, n'apparaîtront pas aussi nettement. Il est donc très important de bien choisir ces deux dimensions parmi l'ensemble des dimensions listées à l'étape précédente. Lorsqu'il y a plusieurs possibilités, il ne faut pas hésiter à toutes les essayer, avant de choisir la meilleure. Dans certains cas, il peut être intéressant d'en garder deux, voire plus, et de les utiliser côte à côte sur chacun des exemples.

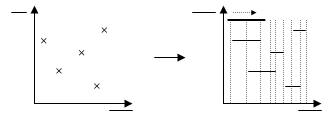
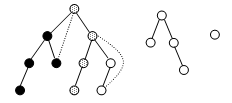
Pour certains types de sujets, il est bon de prendre l'habitude de toujours essayer certaines représentations dites « classiques », qui fonctionnent bien. Ainsi, dans le cas d'un problème de graphe, une représentation naturelle consiste à placer les nœuds à divers endroits et à dessiner simplement les arcs qui relient ces nœuds. Il existe cependant une manière de représenter un graphe qui aide mettre en évidence de nombreuses propriétés : la représentation de Tarjan, qui présente un graphe en mettant en valeur la forêt correspondant à un parcours en profondeur de ce graphe.

Passez donc toujours un certain temps à chercher la meilleure manière de représenter visuellement le problème, cela pourra beaucoup vous aider à trouver sa solution. Appliquez alors cette représentation sur tous vos exemples. Pensez également à bien choisir la manière de représenter les solutions de ces exemples.

4) Générez des exemples et résolvez-les entièrement à la main

Un très bon moyen pour aider vos idées à se former et éviter de vous engager sur de fausses pistes, est d'essayer de résoudre un exemple à la main. Partez de l'exemple fourni dans le sujet, ou d'un exemple encore plus simple, et essayez de résoudre cet exemple à la main simplement à l'aide d'un crayon et d'un papier.

Pendant que vous cherchez à résoudre cet exemple vous-même, faites attention à la manière dont vous procédez. En cherchant à résoudre des exemples, votre cerveau va automatiquement chercher des moyens efficaces qui pourront très probablement être utilisés par un algorithme. Si vous voyez tout de suite la réponse pour cet exemple, demandez-vous pourquoi vous la voyez si facilement. Essayez ensuite sur des exemples plus difficiles, en vous débrouillant pour que la solution ne saute pas aux yeux, mais demande un minimum de travail. La solution ressemble très souvent à ce que vous avez tendance à faire automatiquement à la main : profitez-en !

Essayer plusieurs exemples peut aussi vous aider à bien avoir tous les paramètres du sujet en tête, donc ne peut que vous aider à avoir des idées.

Lorsque vous générez des exemples, ne vous contentez pas de les créer au hasard. Essayez de générer un exemple pour chaque cas particulier auquel vous pouvez penser, et des exemples utilisant des valeurs extrêmes. Générez avant tout des exemples petits et simples, avant d'attaquer des exemples plus gros et compliqués.

Régulièrement au cours de votre réflexion, si vous ne trouvez pas d'algorithme, il ne faut pas hésiter à réessayer à nouveau sur d'autres exemples que vous créez vous-même. Il faut le faire si vous ne trouvez pas tout de suite l'algorithme naïf, et également une fois que vous l'avez, si vous ne voyez pas rapidement d'algorithme efficace. Et même si vous avez un algorithme, il est toujours utile de l'essayer à la main sur des exemples.

Lorsque vous faites cette étape, faites-le proprement et conservez les exemples que vous utilisez, ainsi que la réponse associée. N'ayez pas peur de perdre du temps là-dessus : ces exemples serviront plus tard de tests pour votre solution. Créez dès à présent les fichiers .in et .out avec lesquels vous testerez votre programme. Ceci est d'ailleurs une raison supplémentaire de ne pas bâcler cette étape : tout ce que vous chercherez à la main vous servira plus tard, pour déboguer votre code.

Attention : il est parfois rentable, plutôt que de générer plusieurs exemples à la main, d'écrire une version de l'algorithme naïf permettant de générer de nombreux exemples. Écrire le code d'un algorithme naïf est souvent très simple et les exemples générés ont moins de chances de contenir des erreurs que s'ils étaient écrits à la main. Dans tous les cas, il faut quand même en vérifier un certain nombre à la main pour s'assurer qu'il n'y a pas de bugs dans votre algorithme naïf.

5) Décrivez la solution naïve, puis essayez de l'améliorer

Avant de commencer à chercher des algorithmes puissants et complexes, il faut s'assurer que l'on sait résoudre le problème indépendamment des limites de temps et de mémoire. Le but de cette étape est donc de trouver au moins une manière très simple de résoudre le problème, par un algorithme dit naïf, ou bourrin. Une fois que l'on a exprimé clairement un ou plusieurs algorithmes naïfs, on peut alors essayer de les améliorer, pour obtenir des complexités en temps et mémoire raisonnables.

Lors de l'étape de lecture du sujet, vous aviez reformulé celui-ci sous la forme d'une question. Dans la plupart des problèmes, il est possible de généraliser cette question pour qu'elle puisse exprimer non seulement l'ensemble du problème, mais également des sous-ensembles ou des variantes de ce problème, de telle sorte que l'on puisse utiliser les réponses sur ces sous-ensembles, pour former la réponse du problème complet.

Par exemple, si un problème peut s'exprimer sous la forme de la question suivante :

Quelle est la somme des valeurs fournies en entrée ?

On peut généraliser cette question en :

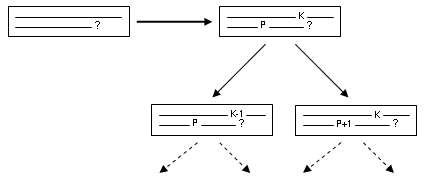
Quelle est la somme des K premières valeurs fournies en entrée ?

La différence avec la question initiale est qu'elle dépend désormais d'un paramètre : le nombre K des valeurs à traiter, là où la question initiale portait sur l'ensemble des valeurs de l'entrée. La nouvelle question généralisée permet toujours de répondre à l'ensemble du problème. Il suffit pour cela d'utiliser comme valeur pour le paramètre K, le nombre total de valeurs de l'entrée.

L'avantage de la question généralisée, est que l'on peut y répondre en la reposant pour une valeur différente : pour répondre à la question « quelle est la somme des K premiers nombres fournis en entrée », on peut reposer la question « quelle est la somme des K − 1 premiers nombres fournis en entrée », et ajouter la K^e valeur de l'entrée à la réponse obtenue. Cela donne donc un algorithme simple pour résoudre ce problème, même s'il n'est pas nécessairement le plus efficace.

L'exemple présenté est un peu simpliste, mais pour peu que l'on trouve la bonne question et la bonne généralisation, la plupart des sujets, mêmes très difficiles, peuvent se résoudre de cette manière. Cela donne une solution récursive souvent très lente, mais qui a le mérite d'être simple et de fonctionner. C'est surtout une très bonne base pour chercher ensuite des solutions plus rapides.

Pour trouver une telle généralisation, ajoutez chaque dimension de l'entrée séparément, comme paramètre de la question initiale. Essayez d'atteindre ainsi une version de la question à laquelle on puisse répondre en la reposant avec des valeurs différentes des paramètres. Dans certains cas, il peut être nécessaire d'utiliser deux, voire plus de paramètres simultanément.

Pour chaque question généralisée qui permet une telle récursion (ne vous arrêtez pas à la première), envisagez l'algorithme naïf correspondant, et calculez sa complexité en temps et en mémoire. Il s'agit généralement d'une fonction récursive dont les paramètres sont ceux de la question, et dont la valeur de retour est la réponse à cette question. Parfois, la solution naïve suffit telle quelle. Dans d'autres cas, une petite modification, profitant d'une propriété mathématique du sujet ou d'une simple astuce peut permettre à la solution exhaustive de fonctionner dans les limites de temps et de mémoire imparties.

Vérifiez donc systématiquement chaque solution naïve, et regardez ce qu'il vous manque pour qu'elle passe en dessous des limites de temps et de mémoire. Cherchez alors ce que cette solution naïve fait en trop, et cherchez un moyen de l'éviter.

Un très bon moyen pour « voir » ce qu'un algorithme naïf fait en trop, consiste à l'exécuter vous-même, à la main, sur un exemple de bonne taille. Il y a de fortes chances qu'à force de l'appliquer mécaniquement, vous remarquiez que certaines opérations pourraient être évitées, et aboutissiez à une idée d'algorithme plus rapide.

Un autre moyen également très efficace pour vous aider à améliorer chaque algorithme naïf, consiste à dessiner une bonne représentation visuelle de ce qu'il fait. On peut dans certains cas voir apparaître très clairement les calculs non indispensables effectués.

Lorsque la solution naïve est simple à programmer, n'hésitez pas à le faire. Cela a plusieurs avantages :

• Vous aurez au moins un programme qui permet d'obtenir quelques points.
• Vous pouvez l'utiliser pour résoudre de nombreux exemples, et remarquer certaines choses en analysant les solutions.
• Il y a des chances qu'une partie du code puisse être reprise telle quelle dans la solution finale, et il est plus facile de déboguer du code d'une solution naïve simple, que de déboguer le même code lorsqu'il fait partie d'un algorithme complexe.
• Quand vous aurez implémenté un meilleur algorithme, vous pourrez comparer les résultats, et vérifier que vous n'avez pas fait d'erreur.
• Si votre algorithme final ne fonctionne pas à tous les coups, vous pourrez intégrer la solution naïve à votre source et l'appeler pour les petits tests, pour vous assurer d'avoir au moins les points correspondants.

6) Résolvez des versions simplifiées du problème, puis généralisez les solutions obtenues

Ce conseil est le plus important de cette liste, il ne faut jamais oublier de l'appliquer.

Si vous ne trouvez pas la solution tout de suite, ou après avoir essayé à la main sur plusieurs exemples, il ne faut pas trop tarder. Le problème est trop difficile pour que vous puissiez trouver facilement la solution, mais il y a un moyen qui peut souvent y conduire. Il s'agit de transformer le problème en le simplifiant, puis d'essayer de résoudre la version simplifiée.

Cette technique est particulièrement efficace pour les raisons suivantes :

• Il est plus facile de trouver les solutions des versions simplifiées, que de résoudre le problème initial.

• Tout algorithme qui résout le problème complet doit nécessairement résoudre les problèmes simplifiés, donc doit au moins faire ce que fait une solution de chacune des versions simplifiées.

• Les idées qui permettent de résoudre les versions simplifiées sont des idées qu'il faut généralement avoir, pour être capable de résoudre le problème initial.

Pour appliquer ce conseil efficacement, il faut :

1. chercher toutes les versions simplifiées du problème qui gardent un sens ;
2. bien choisir quelles versions tenter de résoudre en priorité, et y réfléchir dans cet ordre ;
3. une fois les versions simplifiées résolues, généraliser ces solutions, ou les adapter au problème complet.

Pour effectuer chacune de ces étapes efficacement, il est important de bien s'organiser ; nous allons ci-après décrire comment.

a) Listez les simplifications ayant un sens.

Tous les problèmes ne peuvent pas être simplifiés sans perdre complètement leur nature, mais la plupart le peuvent. Si vous simplifiez un problème puis trouvez la solution de cette version simplifiée, cela vous donne un très bon point de départ pour chercher la solution de la solution complète.

Il y a deux manières d'obtenir des versions simplifiées d'un problème, à appliquer systématiquement :

• Simplifier certaines des dimensions du problèmes. Ceci se fait de manière assez mécanique.

  Pour chacune des dimensions listées à l'étape 2, essayez de :

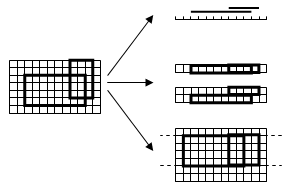
  • la supprimer complètement,
  • la réduire à la plus petite valeur, ou au plus petit sous-ensemble de valeurs pour lequel le problème garde un sens,
  • la fixer à une valeur bien précise (la même valeur pour tous les objets).
  

• Supprimer ou simplifier certaines règles du sujet.

  Cette partie est moins mécanique, mais est en général assez simple à appliquer. Si le sujet interdit certaines opérations, on peut par exemple essayer sans les interdire. Ou s'il y a trois types actions possibles à partir d'une situation, on peut essayer de réduire à un ou deux types d'actions, etc.

Pour chacune de ces simplifications, vérifiez que le nouveau problème obtenu a un sens. S'il en a un, reformulez-le clairement sur votre feuille, éventuellement accompagné d'une petite représentation graphique associée.

b) Choisissez l'ordre dans lequel résoudre les versions simplifiées, et réfléchissez-y dans cet ordre.

Une fois la liste complète des simplifications obtenue par la méthode décrite ci-dessus, classez-la pour les étudier en commençant par celle qui semble la plus intéressante. Il est important de noter que toutes les simplifications ayant un sens sont utiles, et qu'il est nécessaire d'être capable de toutes les résoudre pour pouvoir résoudre le problème entier.

Lorsque vous choissez un version simplifiée du problème, définissez-la précisément, ainsi que les contraintes sur ses variables.

Vous devez ensuite chercher la solution de cette version simplifiée du problème, exactement de la même manière que vous chercheriez la solution d'un problème indépendant. Appliquez tous les conseils de la méthode : recherchez une solution naïve, trouvez une bonne représentation visuelle, essayez des exemples à la main, etc. Il ne faut pas hésiter non plus à simplifier une nouvelle fois le problème, tant que cela a du sens.

Il faut bien vous dire que si vous ne réussissez pas à résoudre la solution simplifiée, vous ne pourrez pas non plus résoudre la version complète. Il faut donc chercher à la résoudre avec autant d'attention que si c'était un problème complet.

c) Généralisez, ou réutilisez les solutions obtenues, pour résoudre le problème initial.

Une fois que vous avez un, ou plusieurs algorithmes permettant de résoudre les versions simplifiées, il faut regarder si on peut les utiliser pour la version complète. Remarquez que s'il y a quelque chose que vous êtes obligé de faire pour résoudre la solution simplifiée, il y a de très grandes chances que vous soyez obligé de le faire également pour la version complète. Si par exemple la solution simplifiée se résout avec un simple algorithme de plus court chemin, la solution évoluée sera donc au moins un algorithme de plus court chemin ; il y a très peu de chances que vous trouviez une version complète qui évite d'utiliser un tel algorithme.

Envisagez toutes les manières de généraliser chaque solution simplifiée obtenue :

• L'appliquer telle quelle, en transformant le problème complet pour qu'il soit équivalent à la version simplifiée.
• L'utiliser pour résoudre une partie du sujet, au sein d'un algorithme plus général.
• Répéter cette solution pour chaque valeur possible de la dimension qui a été supprimée ou réduite.
• Si le problème a des dimensions symétriques, et que la simplification a consisté à supprimer l'une de ces dimensions, appliquer la solution simplifiée selon l'une des dimensions, puis selon l'autre.
• Essayer de généraliser l'idée même qui a donné la solution simplifiée, en réintégrant la dimension supprimée à l'ensemble de l'idée.

N'oubliez pas que chacune des solutions des diverses simplifications est utile, et que la solution complète est souvent une combinaison des solutions simplifiées.

7) Changez de point de vue, en envisageant les algorithmes classiques

Il n'y a pas des millions de types de problèmes différents. On peut en général les classer dans une quinzaine de catégories. Certains types d'algorithmes apparaissent très très souvent. Vous pouvez trouver une liste des algorithmes les plus utilisés, dans le cours « Connaissances nécessaires pour résoudre des problèmes IOI ».

Les algorithmes les plus classiques apparaissent tellement souvent, qu'une des premières choses à faire lorsque vous réfléchissez sur un problème est de regarder si ces algorithmes classiques peuvent aider à résoudre le problème. Cherchez comment vous pouvez les appliquer, et cela vous donnera peut-être la solution.

Il n'est pas nécessaire d'énumérer chacun des algorithmes classiques : on peut le faire par catégorie. Par exemple, pour chaque sujet, essayez de voir s'il est possible de voir le problème comme un problème de graphes, même si cela ne semble pas être le cas à priori : est-ce qu'on peut représenter certaines choses comme des nœuds, et d'autres comme des arcs entre ces nœuds ? Si cela n'a aucun sens, alors aucun des algorithmes de graphes n'a de chance de fonctionner, et vous pouvez éliminer d'un coup toute cette catégorie.

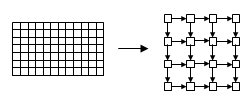
Ceci est aussi particulièrement valable pour les problèmes de type programmation dynamique. De très nombreux problèmes entrent dans cette catégorie. Quel que soit l'exercice, il faut donc passer un certain temps à se demander s'il peut ou non se résoudre par un algorithme dynamique, ne serait-ce qu'en partie.

Si un algorithme classique fonctionne mais ne permet pas de respecter les limites de temps et de mémoire, notez-le quand même. Il pourra vous servir si vous ne trouvez rien de mieux.

Application récursive

Souvent, résoudre un problème nécessite de résoudre plusieurs sous-problèmes, la solution ne s'appliquant pas directement aux données fournies, mais sur les résultats d'un premier calcul devant être fait sur ces problèmes.

Lorsque vous rencontrez un tel sous-problème au cours de votre recherche d'idées, faites de votre mieux pour l'exprimer clairement avec ses propres contraintes, et cherchez-en la solution de manière rigoureuse comme s'il s'agissait d'un problème complet, donc en appliquant de nouveau cette liste de conseils.

Résumé des étapes de la méthode

Vous devez avoir cette liste de conseils parfaitement en tête, et l'appliquer de manière systématique. Si vous ne trouvez pas la solution d'un problème alors que vous n'avez pas appliqué tous ces conseils, vous serez inexcusable.

1. Lisez bien le sujet, et reformulez-le.
2. Faites la liste des dimensions du sujet.
3. Cherchez une bonne représentation visuelle du problème.
4. Générez des exemples, et résolvez-les entièrement à la main.
5. Décrivez la solution naïve, puis essayez de l'améliorer.
6. Simplifiez le problème, puis généralisez les solutions obtenues.
7. Changez de point de vue, en envisageant les algorithmes classiques.

Rappel : appliquez cette méthode à tous les sous-problèmes rencontrés.

Pour chaque idée promettante trouvée au cours de ces étapes, une méthode de clarification/vérification reste à appliquer avant de passer à l'implémentation.